produits scalaire 1ère

Bonjour,

Soit un repère orthonormé (O;i,j).
Soit 2 droites :
D1:−2−5y−3x=0
D2:−3+y−x=0

Grâce au produit scalaire, calculer la mesure non orientée, en radians, de l'angle aigu formé par les 2 droites.
On donnera la réponse approchée à 10^{-2} près.

@hugo-mt_22 ,

Piste de calcul,
Je changement les signes et j'ordonne pour que ce soit plus simple :

$D_1$ ) : $3 x + 5 y + 2 = 0$
$D_2)$ : $x - y + 3 = 0$

Regarde ton cours.
Un vecteur directeur de $D_1)$ est $(−5,3)\overrightarrow{U}\ (-5,3)$
Un vecteur directeur de $D_2)$ est $(1,1)\overrightarrow{V}\ (1,1)$

Tu calcules $U→.V→\overrightarrow{U}.\overrightarrow{V}$ de deux façons :
avec les coordonnés $(X X^{'} + Y Y^{'})$
avec la définition $∣∣U→∣∣×∣∣V→∣∣×cosθ||\overrightarrow{U}||\times ||\overrightarrow{V}||\times cos\theta$

Tu en déduiras $cosθ=XX′+YY′∣∣U→∣∣×∣∣V→∣∣cos\theta=\dfrac{XX'+YY'}{||\overrightarrow{U}|| \times ||\overrightarrow{V}||}$

Tu auras ainsi $cosθcos\theta$ puis $θ\theta$ (valeur approchée calculette, en degrés ou radians, vu que ton énoncé ne le précise pas.

Donne ta réponse si tu souhaites une vérification.

@mtschoon cela fait -2/4

@hugo-mt_22

Je suppose que tu parles du cosinus.
$X X^{'} + Y Y^{'}$ vaut bien -2 mais le produit des normes ne vaut pas 4

@mtschoon C'est -15?

@hugo-mt_22 , non,

Revois ton cours sur la norme d'un vecteur.
Si un vecteur a pour coordonnées (X,Y), sa norme vaut $X2+Y2\sqrt{X^2+Y^2}$

Avec les vecteurs directeurs choisis, tu dois trouver, sauf erreur :
$cosθ=−268cos\theta=\dfrac{-2}{\sqrt{68}}$

En degrés, tu obtiens ainsi , en valeur approchée $104, 04$ °
Il s'agit de l'angle obtus.

Comme l'énoncé veut l'angle aigu, tu donnes :
$180$ °- $104, 04$ °= $75.96$ °

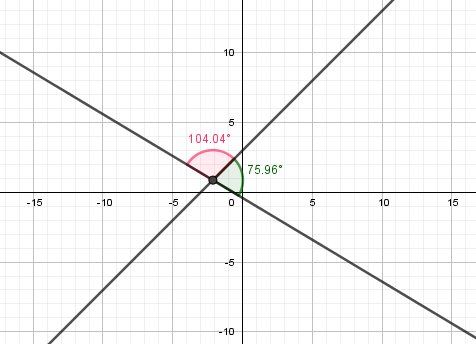
Revois touts tes calculs.