Produit scalaire dans le plan

Bonsoir
J'ai exercice que ja n'arrive pas faire si vous pouvez m'aider
Soit A(5;1) et B(-2;3) deux points du plan.
Détermine et construis l'ensemble (C) des points Mdu plan tels que :MA.MB=0

@serme Bonsoir,

Calcule le produit scalaire en utilisant les coordonnées des vecteurs.

Bonjour,

Evidemment, @serme , tu pourrais trouver le résultat sans calcul,en raisonnant, vu qu'il s'agit d'un produit scalaire nul

$MA→.MB→=0\overrightarrow{MA}.\overrightarrow{MB}=0$ équivaut à dire que les vecteurs $MA→\overrightarrow{MA}$ et $MB→\overrightarrow{MB}$ sont orthogonaux, c'est à dire que le triangle AMB est rectangle en M (ou aplati) c'est à dire que M est sur le cercle (C) de diamètre [AB]

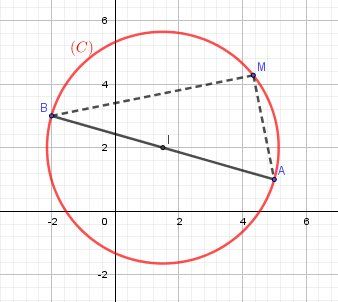
Vu que l'énoncé te donne les coordonnées de A et B, il faut faire les calculs (et bien sûr, tu trouveras le résultat indiqué).

Piste,

Soit $M (x, y)$
$MA→\overrightarrow{MA}$ a pour coordonnées $(5 - x, 1 - y)$
$MB→\overrightarrow{MB}$ a pour coordonnées $(- 2 - x, 3 - y)$
Avec la formule de ton cours pour calculer le produit scalaire de 2 vecteurs dont on connait les coordonnées :
$MA→.MB→=0\overrightarrow{MA}.\overrightarrow{MB}=0$ <=> $(5 - x) (- 2 - x) + (1 - y) (3 - y) = 0$

Tu développes
Tu fais apparaitre des identités remarquables (forme canonique) et tu dois trouver l'équation sous la forme :
$(x−32)2+(y−2)2=534(x-\dfrac{3}{2})^2+(y-2)^2=\dfrac{53}{4}$
Tu tires les conclusions.

Reposte si besoin.

@mtschoon bonsoir
Merci si j'ai des difficulté je vais vous faire signe

D'accord @serme ,
Bons calculs.
Si besoin, je te mets un lien sur l'équation d'un cercle
https://www.nagwa.com/fr/explainers/529134157826/