DM DE MATHS SUR PRODUITS SCALAIRE

[yaya1810]

Bonjour, pourriez vous m'aidez svp car niveaux produits scalaires je ne comprends pas
Voici l'énoncer et les question:
Dans un triangles ABC, on note Ha, Hb, Hc les pieds des hauteurs respectivement issues de A,B et C.
On note a = BC, b = AC, c = AB

1. exprimer l'aire S du triangle ABC de trois manières différentes à l'aide des 3 hauteurs.
2. Déterminer sin(Â), sin(^B) et sin (^C) en fonction de l'aire S et des longueurs a,b et c
3. en déduire la loi des sinus:
   sin(Â)/a = sin(^B)/b = sin(^C)/c = 2S/abc

MERCI A VOUS!

[mtschoon]

@yaya1810 , bonjour,

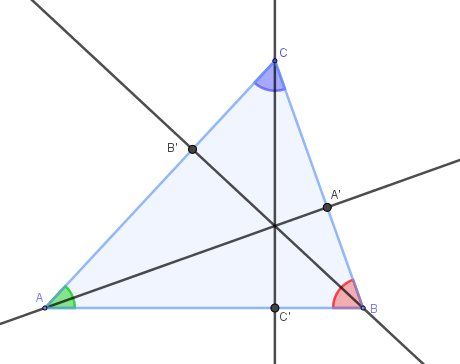
Un schéma pour éclairer.
J'ai changé les notations des pieds des hauteurs pour que ça soit plus simple .
A',B',C' sont les pieds des hauteurs respectivement issues de A, B et C.

Pistes, dans l'ordre des questions posées.

Question 1)

Principe :
$aire{d}^{\prime }untriangle=\frac{1}{2}\times base\times hauteur$
Ainsi

$S=\frac{1}{2}c\times C{C}^{\prime }$

$S=\frac{1}{2}a\times A{A}^{\prime }$

$S=\frac{1}{2}b\times B{B}^{\prime }$

Question 2)

Principe , dans un triangle rectangle
$sinus{d}^{\prime }unangle=\frac{c\hat{o}t\acute{e}oppos\acute{e}}{hypot\acute{e}nuse}$
Ainsi

$sin\hat{A}=\frac{C{C}^{\prime }}{b}$

$sin\hat{B}=\frac{A{A}^{\prime }}{c}$

$sin\hat{C}=\frac{B{B}^{\prime }}{a}$

Il faut transformer en fonction de $S$ pour répondre à la question.

Pour cela , tu utilises les formules trouvées du 1) ( elles sont là pour ça)
$C{C}^{\prime }=\frac{2S}{c}$

$A{A}^{\prime }=\frac{2S}{a}$

$B{B}^{\prime }=\frac{2S}{b}$

En substituant, tu dois obtenir, sauf errrur :
$sin\hat{A}=\frac{2S}{cb}$

$sin\hat{B}=\frac{2S}{ac}$

$sin\hat{C}=\frac{2S}{ab}$

[mtschoon]

Question 3)

Tu isoles $2S$ des formules qui viennent d'êter trouvées , ce qui te donnera 3 égalités :

$2S=cbsin\hat{A}=...=....$

En divisant ces 3 égalités par $abc$, du dois trouver la loi des sinus

$\frac{2S}{abc}=...=...=...$

Je te laisse terminer.

Bons calculs.
Reposte si besoin.

[Black-Jack]

Bonjour,

Avec les notations de mtschoon

S = c/2 * CC' = a/2 * AA' = b/2 * BB'

2S = c * CC' = a * AA' = b * BB'

et avec CC' = b.sin(A) ; AA' = c.sin(B) ; BB' = a.sin(C) remis dans la ligne précédente, on obtient directement :

2S = c * b.sin(A) = a * c.sin(B) = b * a.sin(C)

en divisant par abc ... --> 2S/(abc) = sin(A)/a = sin(B)/b = sin(C)/c