Probabilité conditionnelle
-
MMkdmaria dernière édition par
Bonjour j'ai besoin d'aide pour cet exercice.
Un examen se décompose de questions aux quelles il faut répondre par oui ou
par non
Si un élève connait la réponse, il répond correctement, s’il ignore, il tire à pile ou
face la réponse qu’il inscrira. Un étudiant donné connait 60% du programme.
Quelle est la probabilité pour qu’une réponse juste soit due à ses connaissances
plutôt qu’au hasard ?
Merci d'avance
-
@Mkdmaria Bonjour,
Commence par écrire les probabilités que tu connais, puis calcule la probabilité que l'élève donne la bonne réponse.
Puis tu calcules la probabilité demandée.Indique tes éléments de réponse et/ou tes calculs si tu souhaites une vérification.
-
MMkdmaria dernière édition par
@Noemi
Bonjour, je n'arrive pas à calculer cette probabilité.
Merci cordialement de m'assister
-
Indique les probabilités que l'on peut écrire avec les données de l'énoncé.
Complète :
probabilité (élève connait la bonne réponse) = ....
probabilité (élève ne connait pas la bonne réponse) = ....
probabilité (élève donne la bonne réponse sachant qu'il la connait ) = ....
probabilité (élève donne la bonne réponse sachant qu'il ne la connaît pas) = ....
-
MMkdmaria dernière édition par
@Noemi
probabilité (élève connait la bonne réponse) = 0,6
probabilité (élève ne connait pas la bonne réponse) = 0,4
probabilité (élève donne la bonne réponse sachant qu'il la connait ) = 1/60
probabilité (élève donne la bonne réponse sachant qu'il ne la connaît pas) = 1/2
Merci de vérifier si c'est juste
-
mtschoon dernière édition par mtschoon

Bonjour,
@Mkdmaria , ce 1/60 n'est pas bon.
Je te mets un arbre pour éclairer le raisonnement, si ça peut être utile.
Je t'indique les notations utilisées :
CCC : l'étudiant connait la réponse (cela fait partie de ses connaisances)
C‾\overline CC : l'étudiant ne connait pas la réponse (cela ne fait pas partie de ses connaissances)
JJJ : l'étudiant donne une réponse juste
J‾\overline JJ : l'étudiant ne donne pas une réponse juste.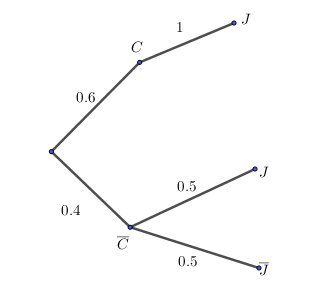
Personnellemnt, je ne trouve pas la phrase de la question bien claire...J'aurais préféré qu'il soit écrit :
Sachant que la réponse est juste, calculer la probabilité qu'elle provienne de ses connaissances.Il faut calculer PJ(C)=P(C∩J)P(J)P_J(C)=\dfrac{P(C\cap J)}{P(J)}PJ(C)=P(J)P(C∩J)
Losque tu auras bien compris l'arbre, avec les données de l'arbre, tu pourras faire le calcul.
Bon calcul.
Donne tes réponses si tu souhaites une vérification.
-
MMkdmaria dernière édition par
@mtschoon
D'après les calculs j'ai trouvé 3/4.
Merci de vérifier cordialement
-
mtschoon dernière édition par

Ta réponse est bonne.
C'est parfait !
-
MMkdmaria dernière édition par
@mtschoon
Merci


-
mtschoon dernière édition par

De rien @Mkdmaria et bon travail.