Patron d'un cône de révolution

[Coumba Diallo]

Pouvez vous m'aider sur cette exercice portant sur le patron du cône de révolution
Exercice : Le schéma ci dessous représente le patron de la partie latérale d'un cône de révolution
1 justifier que le rayon de la base R du cône vaut
R=g ×(1-angle alpha degrés : 360°)
2 Démontrer que la hauteur H vaut
H= R ×racine carré de 1-(a/360°) au carré
3 Exprimer l'aire du cône en fonction de R Et Angle alpha degrés

[Noemi]

@Coumba-Diallo Bonjour,

Il manque le schéma.
A quoi correspond g ?

[Black-Jack]

Bonjour,

Je présume que g est la génératrice du cône ... et d'après les réponses, que alpha est l'angle extérieur au sommet.

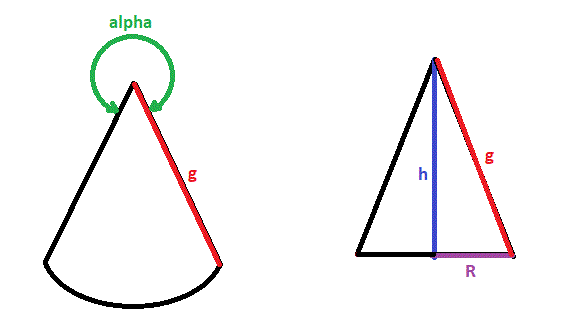
Si oui alors :
1)

L'angle intérieur au sommet = 360° - alpha

La périphérie de la base = 2*Pi * g * (360° - alpha)/360°

qui est aussi égale à 2Pi * R --->

2Pi * g * (360° - alpha)/360° = 2PiR

g * (360° - alpha)/360° = R

g * (1 - alpha/360°) = R

R = g * (1 - alpha/360°) (avex alpha en °)

---

Pour moi tu as fait une faute d'énoncé :

Pythagore --> g² = H² + R²

H² = g² - R²

et avec le résultat du point (1) -->

H² = g² - g² * (1 - alpha/360°)²

H² = g² * (1 - (1 - alpha/360°)²

$H=g\ast \sqrt{1-(1-\frac{\alpha }{360°}{)}^2}$

Ce qui est différent de ce que tu as écrit ...

---

Fais-le après avoir vérifié si il y a aussi une erreur dans l'énoncé de cette partie (R à la place de g ... on non).