Homothéties exercice
-
JJeans yao dernière édition par
Bonsoir j'ai un exercice que je ne comprends pas .
Sur une figure les points M et N sont tels que:
AM(vecteur)=1/3AB(vecteur) et AN(vecteur)1/3AC
I et J sont les milieux respectifs des segments BC et MN .
En utilisant l'homothétie de centre A et de rapport 1/3 démontre que les points A,I et J sont alignés
Merci d'avance
-
@Jeans-yao Bonsoir,
Une piste :
Ecris les vecteurs AI→\overrightarrow{AI}AI et AJ→\overrightarrow{AJ}AJ en fonction des vecteurs AB→\overrightarrow{AB}AB et AC→\overrightarrow{AC}AC.
-
mtschoon dernière édition par mtschoon

Bonjour,
Illustration graphique, si besoin
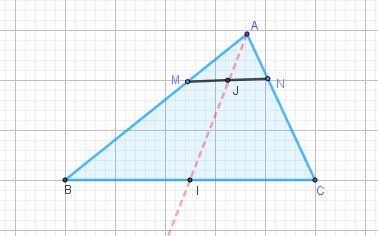
-
mtschoon dernière édition par mtschoon

@Jeans-yao , pour la démonstration , tu as le choix suivant ce que te dis ton cours sur les homothéties.
Si tu n'as que la défintion, tu fais le calcul vectoriel comme te le proposes Noemi (avec la relation de Chasles) et tu trouves AJ→=13AI→\overrightarrow{AJ}=\dfrac{1}{3}\overrightarrow{AI}AJ=31AI, d'où la réponse.
Si ton cours t'indique les propriétés usuelles des homothéties, tu peux les utiliser
Soit hhh l'homothétie de centre A et de rapport 13\dfrac{1}{3}31 : h=H(A,13)h=H(A,\dfrac{1}{3})h=H(A,31)
Par cette homothétie hhh :
L'image de BBB est MMM
L'image de CCC est NNN
Donc,
L'image du segment [BC][BC][BC] est le segment [MN][MN][MN]
L'image du milieu III de [BC][BC][BC] est le milieu JJJ de [MN][MN][MN]Conclusion :
h(I)=J\boxed{h(I)=J}h(I)=J
A étant le centre de l'homothétie hhh, les points A,I,J sont alignésChoisis la méthode qui te convient !