triangles rectangle repère ortonormé

[Aurelee Boutin]

bonjour,
je n'arrive pas trop a réalisé cet exercice alors que je connais les formules, pouvez vous m'aider svp.
voici l'exercice :

1)Dans un repère orthonormé, placer les points : P1 (1;6) , P2 (4;3) , P3 (2;1) ; P4 (0,5 ; 0), P5 (-4; 2) et P6 (-2; 7).
2)tracez les triangles P1P2P3 et P4P5P6. quelle conjecture peut-on faire sur la nature de ces triangles ?
3)vérifier ces conjectures au moyen de l'algorithme
l

la formule est :
j'en ai déduit après avoir tracé les triangles que les deux triangles semblent être des triangles rectangles.
pour le triangle P1P2P3 :
la formule est (xp1 - xp2)*2 - (yp1 -yp2)*2
P1P3 = environ 5,1
P1P2 = environ 4,2
P3P2 = environ 2,8
le triangle n'est donc pas rectangle

pour le triangle P4P5P6 :
P4P6 = environ 7,6
P4P5 = environ 5,4
P5P6 = environ 5,4

j'ai l'impression de m'être trompée pouvais vous m'aider svp

[Noemi]

@Aurelee-Boutin Bonjour,

Vérifie l'écriture de la formule indiquée.

Ne prends pas une valeur approchée mais la valeur exacte.
$P_1{P}_3=\sqrt{2}6$
....

[mtschoon]

Bonjour,

@Aurelee-Boutin , je te joins un schéma si le tien n'est pas clair

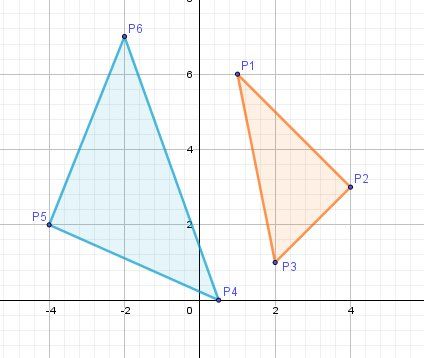
Le triangle P1P2P3 semble rectangle en P2
Utilise la réciproque du théorème de Pythagore pour le prouver
Tu dois trouver, après calcul :
$P1P{2}^2=18$
$P1P{3}^2=26$
$P2P{3}^2=8$
Donc : $P1P{3}^2=P1P{2}^2+P2P{3}^2$

Tu traites de même le triangle $P4P5P6$

Si tu as besoin d'un algorithme , tu peux consulter ici éventuellement :
https://forum.mathforu.com/topic/32911/devoir-de-maths-sur-les-repères-orthonormé
Cet algorithme est écrit avec la syntaxe Python, mais tu peux l'écrire avec la syntaxe dont tu as l'habitude.

[Aurelee Boutin]

Ce message a été supprimé !

[Aurelee Boutin]

@mtschoon a dit dans triangles rectangle repère ortonormé :

Bonjour,

@Aurelee-Boutin , je te joins un schéma si le tien n'est pas clair

Le triangle P1P2P3 semble rectangle en P2
Utilise le théorème de Pythagore pour le prouver
Tu dois trouver, après calcul :
$P1P{2}^2=18$
$P1P{3}^2=26$
$P2P{3}^2=8$
Donc : $P1P{3}^2=P1P{2}^2+P2P{3}^2$

Tu traites de même le triangle $P4P5P6$

Si tu as besoin d'un algorithme , tu peux consulter ici éventuellement :
https://forum.mathforu.com/topic/32911/devoir-de-maths-sur-les-repères-orthonormé
Cet algorithme est écrit avec la syntaxe Python, mais tu peux l'écrire avec la syntaxe dont tu as l'habitude.

si j'utilise l'algorithme, je dois écrire mes calculs comme ceux de l'algorithme, je dois les convertir en écriture python ? c'est bien ça ? (car oui c'est le même que j'utilise en classe)

[mtschoon]

@Aurelee-Boutin , si tu utilises Python en classe, tu n'as rien à faire de plus.
Dans l'algorithme donné par Aurelee Boutin , le triangle s'appelle $ABC.$
Tu peux l'appeler $P_1{P}_2{P}_3$ si tu préfères.