asymptotes fonction f(x) = x racine de (x-1/x+1)

Bonjour,je suis occupée à refaire un examen de maths que je vais devoir repasser et j'ai besoin d'aide pour un exercice sur la fonction f(x) = x racine de (x-1/x+1) et j'ai besoin d'aide pour définir les asymptotes de cette fonction svp

@yasmine_afk Bonjour,

Quel est le domaine de définition de cette fonction ?
Comment détermine t'on les asymptotes d'une fonction ?

je sais que le domaine de cette fonction est -1;1 mais en soit ce n'est pas ça qui me bloque. Les asymptotes aussi je sais les faire mais le x devant la racine me perturbe. Je ne sais pas quoi en faire

@yasmine_afk

Je suppose que pour le domaine de définition, tu as voulu dire : $R−[−1;1[\mathbb{R}- [-1;1[$ ?

Indique tes calculs pour les limites.

AV:
lim tendant vers -1: -1raccarré (-1) -1/-1+1= -1rac-2/0 = +- l'infini donc A.V en -1
lim tendant vers 1: 1rac (1)-1/1+1= 1rac0/2 = pas d'A.V en 1

AH: y'en a pas
A.O: lim tendant vers +- l'infini
m: xrac x-1/X+1/x
et de là je bloque. Fin je sais que mon raisonnement est faux.

Bonjour,

@yasmine_afk, je regarde un peu tout ça,

Sans parenthèses, l'expression que tu donnes n'est pas bien écrite en texte.
Si possible, écris correctement en Latex :
$f(x)=xx−1x+1f(x)=x\sqrt{\dfrac{x-1}{x+1}}$ ; c'est visiblement ce que tu voulais écrire.

J'espère @yasmine_afk que tu as fait l'étude soignée de la fonction pour savoir où il faut que tu cherches les asymptotes éventuelles.

Comme te l'a indiqué @Noemi , l'ensemble de définition que tu donnes n'est pas bon
$Df=]−∞,−1[∪[1,+∞[D_f=]-\infty,-1[\cup [1,+\infty[$ (regarde bien les crochets)

Pour avoir une asymptote possible, il faut avoir une branche infinie.
$1$ apartient à $D_f$ .
$f (1) = 0$
Pas de branche infinie donc à forciori, pas d'asymptote

$lim⁡x→−1(x<−1)f(x)=−∞\boxed{\displaystyle \lim_{x\to -1 (x\lt -1)}f(x)=-\infty}$
La droite d'équation $x = - 1$ est donc asymptote "verticale" à la courbe.
Revois ce que tu as indiqué dans ton explication, car il ne faut pas remplacer $x$ par $- 1$ mais il faut faire tendre $x$ vers -1 (par valeurs inférieures à -1, vu l'ensemble de définition)

@yasmine_afk, je t'indique une réponse possible lorsque $x$ tend vers $+∞+\infty$ (et tu pratiques de même pour $−∞-\infty$ )

$lim⁡x→+∞f(x)=+∞\displaystyle \lim_{x\to +\infty}f(x)=+\infty$ donc possibilité d'une asymptote oblique d'équation $y = a x + b$

$lim⁡x→+∞f(x)x=1\displaystyle \lim_{x\to +\infty}\dfrac{f(x)}{x}=1$ (facile à trouver) donc $a = 1$

Ensuite, tu dois chercher $lim⁡x→+∞[f(x)−ax]\displaystyle \lim_{x\to +\infty}[f(x)-ax]$
Si cette limite est un réel $b$ , l'équation de l'asymptote oblique sera $y = a x + b$

(j'espère que cette propriété est dans ton cours)

On cherche donc $lim⁡x→+∞[f(x)−x]\displaystyle \lim_{x\to +\infty}[f(x)-x]$
Si tu ne te trompes pas , tu dois trouver $b = - 1$ donc asymptote oblique d'équation $y = x - 1$ lorsque $x$ tend vers $+∞+\infty$

Cette limite n'est pas si facile que ça à trouver, car suivant les transformations, on peut tomber sur une indétermination.

Je te suggère d'utiliser le conjugué de l'expression (tu multiplies numérateur et dénominateur par l'expression $(xx−1x+1+x)(x\sqrt{\dfrac{x-1}{x+1}}+x)$ et d'utiliser l'identité remarquable $a-b)(a+b)=a^2-b^2$

Je te mets quelques détails de calcul mais ce serait trop long de tout écrire.
A toi de faire tous les calculs.

$f(x)−x=xx−1x+1−xf(x)-x=x\sqrt{\dfrac{x-1}{x+1}}-x$

$f(x)−x=(xx−1x+1−x)(xx−1x+1+x)xx−1x+1+xf(x)-x=\dfrac{(x\sqrt{\dfrac{x-1}{x+1}}-x)(x\sqrt{\dfrac{x-1}{x+1}}+x)}{x\sqrt{\dfrac{x-1}{x+1}}+x}$

$f(x)−x=x2(x−1x+1)−x2xx−1x+1+xf(x)-x=\dfrac{x^2(\dfrac{x-1}{x+1})-x^2}{x\sqrt{\dfrac{x-1}{x+1}}+x}$

Après calculs, simplifications, tu dois arriver à :
$f(x)−x=−2x2(x+1)(xx−1x+1+x)f(x)-x=\dfrac{-2x^2}{(x+1)(x\sqrt{\dfrac{x-1}{x+1}}+x)}$

En simplifiant numérateur et dénominateur par $x^2$ , tu dois arriver à :
$f(x)−x=−2(1+1x)(x−1x+1+1)f(x)-x=\dfrac{-2}{(1+\dfrac{1}{x})(\sqrt{\dfrac{x-1}{x+1}}+1)}$

En prenant la limite en $+∞+\infty$

$lim⁡x→+∞[f(x)−x]=−22=−1\displaystyle \lim_{x\to +\infty}[f(x)-x]=\dfrac{-2}{2}=-1$ donc $b = - 1$

D'où asymptote oblique d'équation $y=x−1\boxed{y=x-1}$

Pour $y$ tendant vers $−∞-\infty$ , tu dois trouver la même asymptote.

Bon travail.

Je te joins une représentation graphique.

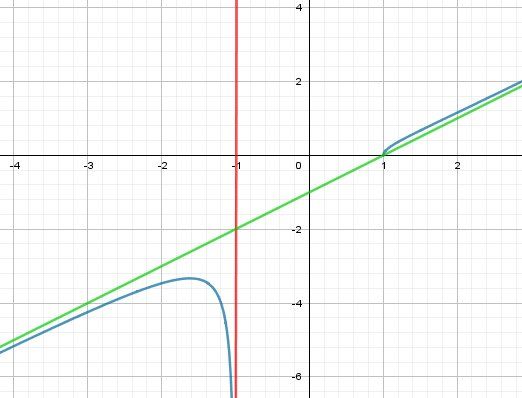
La coube est en bleu
l'asymptote verticale est en rouge
l'asymptote oblique est en vert.

@yasmine_afk, si tu as besoin d'un cours sur le asymptotes, tu peux regarder là :

https://www.ukonline.be/cours/math/basehigher-summary/chapitre12-2

@mtschoon Merci milles fois pour vos explications ça m'aide énormément !!
Je refaire attentivement toutes les étapes moi-même.
Bonne soirée à vous.

Bonjour,

Il fut un temps où écrire f(x) = x racine de (x-1/x+1) comme identique à $x.\sqrt{\frac{x-1}{x+1}}$ était synonyme d'un carton rouge immédiat.

Maintenant, plus personne n'y fait attention ...

Ce que tu as écrit correspond à $x.\sqrt{x - \frac{1}{x} + 1}$ , ce qui est fondamentalement différent.

@yasmine_afk a dit dans asymptotes fonction f(x) = x racine de (x-1/x+1) :

@mtschoon Merci milles fois pour vos explications ça m'aide énormément !!
Je refaire attentivement toutes les étapes moi-même.
Bonne soirée à vous.

@yasmine_afk . de rien !

Effectivement, tu dois refaire toutes les étapes pour être sûr de maîtriser.

Bon courage pour ton examen