Equation tangente et position relative de la courbe
-
nathan_n dernière édition par nathan_n
Non mais il y a un second exercice (que j'ai réussi) mais sur lequel j'ai un doute:
Exercice 2 :- Déterminer l’équation de la tangente à la courbe représentative de la fonction racine carrée au point d’abscisse 4.
- Étudier la position relative de la courbe représentative de la fonction racine carrée par rapport à cette tangente
- f'(4)(x-4)+f(4)=(1/4)x+1 là je suis sûr de moi
- Là je pense qu'il faut faire f(x)-((1/4)x+1 )=√𝑥-(1/4)x-1
Et ensuite il faut étudier le signe de cette expression mais je ne suis pas sûr.
-
Pour un second exercice, il faut proposer un autre sujet. Je vais déplacer ces messages.
Les résultats sont corrects. Etudie le signe de l'expression.
-
nathan_n dernière édition par nathan_n
Merci. Mais je n'arrive pas à déterminer le signe de √𝑥-(x/4)-1. Il suffit de résoudre une simple inéquation mais je ne sais pas pourquoi je ne parviens pas à isoler x. A moins de séparer √𝑥 et -(x/')-1 puis de faire le tableau de signe. Dans ce cas là, l'expression > 0 sur [0;+oo]
-
Etudie les variations de la fonction g(x)=x−x4−1g(x) = \sqrt x-\dfrac{x}{4}-1g(x)=x−4x−1
-
nathan_n dernière édition par
Après avoir longtemps cherché, je ne trouve pas la solution. J'ai l'impression que c'est tout simple mais je n'y arrive pas.
-
As-tu calculé la dérivée : g′(x)=12x−14=2−x4xg'(x)= \dfrac{1}{2\sqrt x}-\dfrac{1}{4}=\dfrac{2-\sqrt x}{4\sqrt x}g′(x)=2x1−41=4x2−x ?
Tu étudies le signe de la dérivée : + 0 -
puis les variations de la fonction : croissante puis décroissante.
Les limites de cette fonction montrent que la fonction est .....
Tu conclus.
-
nathan_n dernière édition par
D'accord.
Donc après calculs on a la tangente qui est au dessus de Cf sur ]-oo;0[U]4;+oo[ et en dessous de Cf sur ]0;4]
C'est ça ?
-
Non,
La fonction n'est définie que sur l'intervalle [0;+∞[[0;+\infty[[0;+∞[ et la fonction dérivée sur ]0;+∞[]0;+\infty[]0;+∞[
Sur l'intervalle [0;4[[0;4[[0;4[, g(x)g(x)g(x) varie de -1 à 0 et
g(4)=0g(4)= 0g(4)=0
sur l'intervalle ]4;+∞[]4;+\infty[]4;+∞[, g(x)g(x)g(x) varie de 0 à −∞-\infty−∞;
Conclusion g(x)≤0g(x) \leq0g(x)≤0
d'ou la tangente est toujours au dessus de CfC_fCf.
-
mtschoon dernière édition par mtschoon

Bonjour,
Illustration graphique.
La courbe est en rouge
La tangente en A(4,2) est en bleu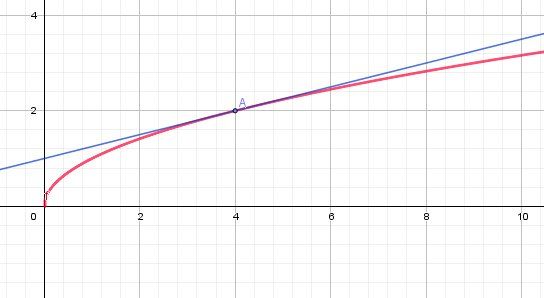
-
nathan_n dernière édition par
D'accord. Merci à tous pour vos réponses !
Bonne soirée.