Le nombre complexe j

Bonsoir,
Je noterai le conjugué de J : j pour la distinction
J’ai donc dans mon exo J est le nombre complexe vérifiant :
j= J^2
J^2 + j = -1
J + j = -1
J^3 = 1
Et on me demande de calculer J, sachant que je dois le trouver en forme exponentielle re^i θ
Je n’arrive pas à trouver le raisonnement à avoir pour l’instant par propriété je n’ai pu que déduire que Re(J) =-1/2
Mais pas sure de l’utilité du résultat
Merci d’avance pour toute aide
Bonne soirée

@yasmi16 Bonsoir,

Vérifie l'énoncé, à partir des deux premières relations, on déduit $2 j = - 1$ .

Bonjour,

@yasmi16 , pour plus de clarté, j'écris ton énoncé avec les notations usuelles des conjugués.

Si j'ai bien lu :

$Jˉ=J2\bar J=J^2$ (formule 1)
Ta formule 2 donnée n'est pas bonne. Il y a une erreur d'écriture,
ça devrait être $J^2+J=-1$
$\bar J=-1$ (formule 3)
$J^3=1$ (formule 4)

Tu cherches $J$ satisfaisant à ces 4 conditions.

Piste possible (à expliciter),

Je te propose de commencer par utiliser la formule 4
$J3=1\boxed{J^3=1}$
$J$ est donc une racine cubique de 1 (il y en a 3)
Si tu n'as pas de cours sur ce sujet, tu fais le calcul en passant par la forme exponentielle (vu que c'est la forme demandée dans ton énoncé)
Soit $J=reiθJ=re^{i\theta}$

$J^3=1$ <=> $r3e3iθ=1e0r^3e^{3i\theta}=1e^0$
d'où :
$r^3=1$ <=> $r = 1$
$3θ=0+2kπ,k∈Z3\theta=0+2k\pi, k\in Z$ <=> $θ=2kπ3,k∈Z\theta=\dfrac{2k\pi}{3}, k\in Z$

Au final, tu obtiens trois valeurs :
$z_0=1$ (pour $k = 0$ ) (image A sur le cercle trigonométrique)
$z1=e2iπ3z_1=e ^{\dfrac{2i\pi}{3}}$ (pour $k = 2$ ) (image B sur le cercle trigonométrique)
$z1=e4iπ3z_1=e^{\dfrac{4i\pi}{3}}$ (pour $k = 3$ ) (image C sur le cercle trigonométrique)

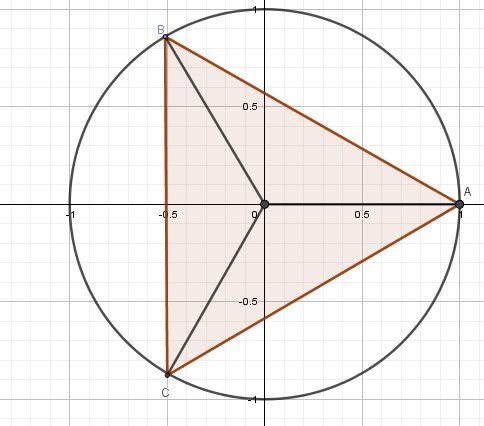
Parmi ces 3 valeurs, tu cherches celle(s) qui satisfait aux formules 1,2(modifiée),3.
Si besoin, pour t'aider à cette recherche , tu peux éventuellement mettre $z_0,z_1,z_2$ sous forme algébrique
$z_0=1$
$z1=−12+i32z_1=-\dfrac{1}{2}+i \dfrac{\sqrt 3}{2}$
$z2=−12−i32z_2=-\dfrac{1}{2}-i \dfrac{\sqrt 3}{2}$

Je te laisse trouver, parmi ces trois valeurs, celle(s) qui convient à $J$
Tu peux donner ta réponse pour vérification si tu le souhaites.

Bonjour,

Autrement. (avec l'énoncé corrigé selon les indications du message de mtschoon)

(2) --> J² + J + 1 = 0 et donc les seuls candidats solutions sont J = -1/2 - i.V3/2 et J = -1/2 + i.V3/2

On calcule donc très facilement :

J = -1/2 +/- i.V3/2
J² = -1/2 -/+ i.V3/2
J(barre) = -1/2 -/+ i.V3/2
J³ = J² * J = (-1/2 -/+ i.V3/2) * (-1/2 +/- i.V3/2) = 1

On vérifie alors (1), (3) et (4) pour ces 2 possibilités de solutions ..., tout fonctionne pour les 2 solutions

Et donc ...

Toutes distractions incluses.

@mtschoon
Bonjour,
Oui en effet je m’étais trompé en tapant
Merci c’est beaucoup plus clair pour moi
Et la bonne réponse c’est j = -1/2 + i rac3/2
Bonne journée

@Black-Jack
Merci beaucoup d’avoir pris le temps
C’est clair maintenant
Passez une bonne journée

@yasmi16 , oui la valeur de $j$ que tu donnes est bonne.

C'est la notation usuelle de $j$ en mathématiques (je précise), car dans certaines autres disciplines $j$ est utilisé autrement ( à la place de $i$ ).

$j=e2iπ3=−12+i32j=e^{\dfrac{2i\pi}{3}}=-\dfrac{1}{2}+i\dfrac{\sqrt 3}{2}$

Regarde le lien ici
https://fr.wikipedia.org/wiki/J_(nombre_complexe)

Mais , si tu fais toutes les vérifications des 4 conditions, dans cet exercice, tu peux aussi donner à $j$ la valeur
$e4iπ3=−12−i32e^{\dfrac{4i\pi}{3}}=-\dfrac{1}{2}-i\dfrac{\sqrt 3}{2}$

Ces deux valeurs sont des valeurs conjuguées.

Dans ton exercice, tu dois donner les deux valeurs possibles.

Remarque : Si ton énoncé avait précisé, en plus, en 5ième condition, que la partie imaginaire de $j$ était strictement positive ( ce qui aurait été heureux, je pense...) tu n'aurais trouvé que $j=e2iπ3=−12+i32j=e^{\dfrac{2i\pi}{3}}=-\dfrac{1}{2}+\dfrac{i\sqrt 3}{2}$ , qui est la valeur usuelle.