Polynôme problème de triangle

[math58004]

Bonjour j'ai un exercice à faire j'ai besoin d'aide svp

ABCD est un rectangle tel que AB=1 et AD=2. I est le milieu de [AB].
Pour tout point M du segment [AD], on pose AM = $x$

1. Quelles valeurs peut prendre $x$?
   Rép: $x=[0;2]$

2. On pose $f(x)=M{I}^2+M{C}^2$
   Exprimer $f(x)$ en fonction de $x$.

Je sais pas du tout ce que je dois utiliser, peut-être le théorème de Pythagore..?

3. Dresser le tableau de variation de la fonction $f$

4. On se propose de déterminer les valeurs de $x$ pour lesquelles le triangle $IMC$ est rectangle en $M$.

a)Montrer que le triangle IMC est rectangle si, et seulement si, $f(x)=\frac{17}{4}$

b) Déterminer les valeurs de $x$ pour lesquelles le triangle $IMC$ est rectangle.

[Noemi]

@math58004 Bonjour,

Oui, applique le théorème de Pythagore.

[mtschoon]

Bonjour,

Un schéma, pour éclairer.

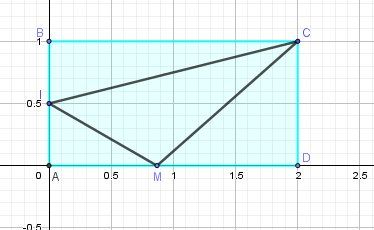
Oui, @math58004 ,comme te le dit @Noemi, il faut utiliser le théorème de Pythagore, pas dans le triangle $IMC$ (qui n'est pas toujours rectangle), mais dans les triangles $IAM$ et $MDC$ qui sont rectangles, pour déterminer l'expression de $f(x)$

[mtschoon]

@math58004 , j'espère que tu as trouvé l'expression de $f(x)$

Un petit plus, si besoin.

$M{I}^2=M{A}^2+A{I}^2=x^2+(\frac{1}{2}{)}^2$

$M{C}^2=M{D}^2+D{C}^2=(2-x{)}^2+(1{)}^2$

Tu peux réduire chaque expression et en les ajoutant, tu obtiens $f(x)$

Sauf erreur, tu dois trouver : $f(x)=2x^2-4x+\frac{21}{4}$

Vérifie tout ça et essaye de poursuivre.

Reposte si besoin.