Variation d'une suite

Salut je suis nouvelle j'ai une question plutôt besoins d'aide je dois étudier le sens de variation de la suite $Un=5n+1n+2U_n=\dfrac{5n+1}{n+2}$
MERCI POUR VOTRE AIDE

Relation mise en forme par la modération du forum.

@thestraw0 , bonjour.

Sans trait de fraction, tu dois mettre des parenthèses pour bien distinguer numérateur et dénominateur.
Je pense qu'il s'agit de $Un=5n+1n+2U_n=\dfrac{5n+1}{n+2}$

$Un+1=5(n+1)+1n+1+2=5n+6n+3U_{n+1}=\dfrac{5(n+1)+1}{n+1+2}=\dfrac{5n+6}{n+3}$

Je te conseille de calculer $U_{n+1}-U_n$ ( tu réduis au même dénominateur $(n + 2) (n + 3)$ et tu simplifies le numérateur obtenu), puis tu trouves le signe de cette différence.
Ensuite, tu tires la conclusion.

Reposte si besoin.

@thestraw0 , j'espère que tu as trouvé :

$Un+1−Un=9(n+2)(n+3)U_{n+1}-U_{n}=\dfrac{9}{(n+2)(n+3)}$

Vu que tu parles de suites, je suppose que $n∈Nn\in N$

Tu dois justifier que $Un+1−Un>0U_{n+1}-U_{n}\gt 0$ et déduire le sens de variation de cette suite.

Illustration des premiers termes

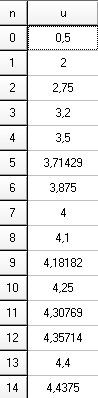
Bien sûr, cette suite converge vers 5 (mais ce n'est pas demandé)

je vois mais perso j'ai trouvé (3/(n+2)(n+3))

@thestraw0 , vérifie ton calcul pour trouver ton erreur.

Je détaille un peu

En réduisant au même dénominateur

$Un+1−Un=(5n+6)(n+2)−(5n+1)(n+3)(n+2)(n+3)U_{n+1}-U_n=\dfrac{(5n+6)(n+2)-(5n+1)(n+3)}{(n+2)(n+3)}$

$Un+1−Un=(5n2+10n+6n+12)−(5n2+n+15n+3)(n+2)(n+3)U_{n+1}-U_n=\dfrac{(5n^2+10n+6n+12)-(5n^2+n+15n+3)}{(n+2)(n+3)}$

$Un+1−Un=(5n2+16n+12)−(5n2+16n+3)(n+2)(n+3)U_{n+1}-U_n=\dfrac{(5n^2+16n+12)-(5n^2+16n+3)}{(n+2)(n+3)}$

Il te reste à simplifier le numérateur et tu trouveras :

$Un+1−Un=9(n+2)(n+3)U_{n+1}-U_n=\dfrac{9}{(n+2)(n+3)}$

Bon calcul.

Une remarque : tu as posté en Terminale scientifique, mais j'aurais pensé qu'il s'agit plutôt d'un exercice de Première.
Tu t'es peut-être trompé(e) de rubrique.

okay merci beaucoup je comprend mieu et je ne me suis pas tromper je suis en, terminal spé math et j'ai eu cette exo

C'est bien @thestraw0 , si tu comprends mieux.

Merci pour la précision. Peut-être n'as tu pas traité ce type de question sur les suites en Première, ce qui explique ta difficulté.

Si besoin, tu peux regarder un cours :
https://www.mathforu.com/premiere-s/les-suites-en-1ere-s/

Bon travail !

Merci à la modération pour la mise en forme de la formule de l'énoncé.