Determiné Polynome du second degrés
-
Antho. 77 Oliveira dernière édition par
Bonjour J'ai un dm pour demain mardi mais je comprend rien pouvez vous m'aider ?
l'énoncé :
P(x) = 6x4 - 41x3 + 69x²+6x-40
et la première question c'est : Déterminé un polynôme Q tel que, pour tout réel x: P(x)= (x-1)(x-4)Q(x)
Les autres question je me débrouillerai!
Merci d'avance
PS : les nombres devant les x sont des puissances
-
@Antho-77-Oliveira Bonjour,
Une piste :
Pose Q(x)=ax2+bx+cQ(x)= ax^2+bx+cQ(x)=ax2+bx+c
Développe (x−1)(x−4)(ax2+bx+c)(x-1)(x-4)(ax^2+bx+c)(x−1)(x−4)(ax2+bx+c)
Puis identifie chaque termes avec P(x)P(x)P(x).
-
Antho. 77 Oliveira dernière édition par
Bah c'est ce que j'ai fait.
Mais j'arrive a une expression énorme que je peux plus simplifier ni factoriser
Et Quand je refais mon développement je me retrouve avec la même expression
-
En développant tu dois trouver :
ax4+(b−5a)x3+(c−5b+4a)x2+(−5c+4b)x+4cax^4+(b-5a)x^3+(c-5b+4a)x^2+(-5c+4b)x+4cax4+(b−5a)x3+(c−5b+4a)x2+(−5c+4b)x+4c
Le terme en x4x^4x4 est ax4ax^4ax4 qui correspond à 6x46x^46x4, donc a=6a = 6a=6.
Le terme en x3x^3x3 est b−5ab-5ab−5a, donc b−5a=−41b-5a=-41b−5a=−41
Le terme en x2x^2x2 est (c−5b+4a)x3(c-5b+4a)x^3(c−5b+4a)x3, donc c−5b+4a=69c-5b+4a= 69c−5b+4a=69
Le terme en xxx est −5c+4b-5c+4b−5c+4b, donc −5c+4b=6-5c+4b=6−5c+4b=6
Le terme constant est 4c4c4c, donc 4c=−404c = -404c=−40, donc c=...c = ...c=...Je te laisse écrire tes calculs.
-
Antho. 77 Oliveira dernière édition par
Merci beaucoup , ca m'aide énormément !
Je complète la suite !
-
Antho. 77 Oliveira dernière édition par
Mais pour x3 c'est pas (b-5a) ?
-
Antho. 77 Oliveira dernière édition par Antho. 77 Oliveira
c = -10 déjà, après comment je trouve Q(x) car j'ai toujours a, b, c et d ?
Ou alors x² est b ?
-
Oui pour x3x^3x3
Sauf erreur tu dois trouver :
a=6a= 6a=6 ; b=−11b= -11b=−11 ; c=−10c= -10c=−10
Et tu en déduis Q(x)=....Q(x) = ....Q(x)=....
-
Antho. 77 Oliveira dernière édition par
Je déduis que Q(x) = 6x²-11x-10 ?
-
mtschoon dernière édition par

Bonjour,
Je regarde ta réponse @Antho-77-Oliveira , vu que je passe par là.
Oui, je trouve comme t'a indiqué @Noemi et comme tu l'indiques.
Tu peux d'ailleurs factoriser Q(x)Q(x)Q(x) et trouver 4 facteurs du premier degré .
Sauf erreur :
P(x)=(x−1)(x−4)(2x−5)(3x+2)P(x)=(x-1)(x-4)(2x-5)(3x+2)P(x)=(x−1)(x−4)(2x−5)(3x+2)
-
Antho. 77 Oliveira dernière édition par
Il faut que je trouve Q(x) avec : (2x-5)(3x+2)
Ce qui donne 6x²-11x-10
Mais comment on sait que Q(x) est égale a (2x-5)(3x+2)
-
Pour déterminer la factorisation du polynôme, tu résous l'équation :
6x2−11x−10=06x^2-11x-10= 06x2−11x−10=0
-
mtschoon dernière édition par mtschoon

Re-bonjour,
@Antho-77-Oliveira , si ton cours n'est pas clair pour factoriser un polynôme du second degré (méthode de Première, sans passer par le forme canonique), tu peux regarder ici :
https://www.mathforu.com/premiere-s/le-second-degre-2eme-partie/
-
Antho. 77 Oliveira dernière édition par
Oui j'ai trouver merci beaucoup Pour l'aide !!!!!
-
Parfait si tu as tout compris.
-
mtschoon dernière édition par

Bonjour,
Pour vérifier les valeurs qui annulent P(x)P(x)P(x), tu peux faire la représentation graphique de la fonction PPP
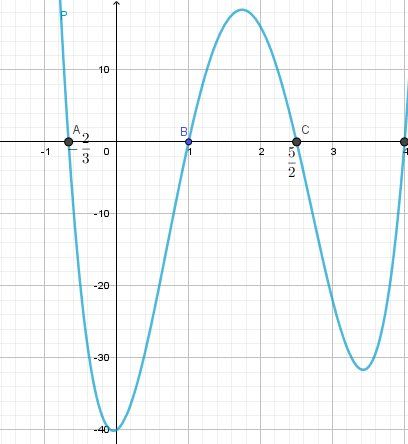
Bon travail.