Calcul de dérivée terminale s

Bonjour j’ai un exercice à faire mais je en comprends pas comment faire

Je dois calculer la dérivée de cette fonction
G(x)=exp(2x)-exp(x)-x
Je ne sais pas par où commencer ni même quoi faire

@hugopep87 , bonjour,

la dérivée de $e^{u(x)}$ est $eu(x)×u′(x)e^{u(x)}\times u'(x)$
la dérivée de $e^x$ est $e^x$
la dérivée de $x$ est $1$

Donc : pour $G(x)=e^{2x}-e^x-x$

$G'(x)=2e^{2x}-e^x-1$

@hugopep87 , si c'est la fonction exponentielle qui te pose problème, tu peux consulter un cours ici: //www.mathforu.com/terminale-s/fonctions-exponentielles-et-logarithme-pour-terminale-s/

@mtschoon

Merci beaucoup

De rien @hugopep87 et bon travail.

@mtschoon re bonjour j’ai un problem pour dresser mon tableau de variation je ne comprends pas comment faire avec les exponentielles

@hugopep87 , comme pour toute fonction, il faut que tu trouves le signe de $G^{'} (x)$

$G'(x)=2e^{2x}-e^x-1$

Pour résoudre $G^{'} (x) = 0$ , tu peux poser $X=e^x$

Equation auxiliaire : $2X^2-X-1=0$

Equation du second degré que tu résous.

Sauf erreur , deux solutions $X 1 = 1$ et $X2=−12X_2=-\dfrac{1}{2}$
Retour à $x$ :
$e^x=1$ <=> $x = 0$
$ex=−12e^x=-\dfrac{1}{2}$ Impossible car pour tout $x$ réel, $ex>0e^x\gt 0$

La dérivée s'annule donc seulement pour $x = 0$

Pour savoir son signe sur $]−∞,0[]-\infty,0[$ et sur $]0,+∞[]0,+\infty[$ , un test simple par intervalle suffit .
Par exemple, $x = - 1$ et $x = 1$

Tu pourras ainsi avoir le signe de la dérivée d'où le sens de variation de la fonction.

Reposte si besoin.

@mtschoon je n’ai pas compris le truc du test de l’intervalle

$G'(1)=2e^2-e-1$
$G′(1)≈11G'(1)\approx 11$
$G′(1)>0G'(1)\gt 0$
$\gt 0$ pour $x∈]0,+∞[x\in]0,+\infty[$

Lorsque tu as compris, tu peux faire pareil pour $x = - 1$ pour trouver le signe sur $]−∞,0[]-\infty,0[$

@mtschoon merci pour ça mais ducoup ensuite on me demande de montrer que Un est croissante en ayant remarquer que Un+1-Un=g(Un)
Et je n’arrive pas à faire ça

@hugopep87 et on dit que Un+1=exp(2Un)-exp(Un)

@hugopep87 j’ai ensuite démontrer par recurence que Un<=0

@hugopep87 , il faut de la rigueur...

Tu passes à une question sans avoir terminé la prcédente ?

J'espère que tu as fait le tableau de variation de la fonction $G$
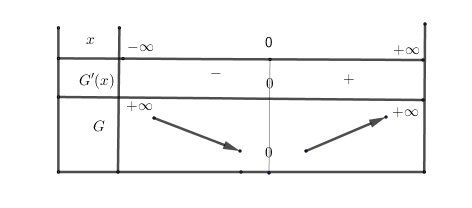
Les limites ne sont peut-être pas obligatoires

@hugopep87 a dit dans Calcul de dérivée terminale s :

@mtschoon merci pour ça mais ducoup ensuite on me demande de montrer que Un est croissante en ayant remarquer que Un+1-Un=g(Un)
Et je n’arrive pas à faire ça

Je réponse à cette question.

$U_{n+1}=e^{2U_n}-e^{U_n}$
donc :
$U_{n+1}-U_n=e^{2U_n}-e^{U_n}-U_n$

Regarde bien l'expression de $G (x)$ et tu peux dire que :
$Un+1−Un=G(Un)\boxed{U_{n+1}-U_n=G(U_n)}$

Conséquence
D'après le tableau de variation de $G$ , tu peux déduire que $\ge 0$ donc $G(Un)≥0G(U_n)\ge 0$ donc $Un+1−Un≥0U_{n+1}-U_n\ge 0$ donc la suite $U_n)$ est croissante.

Essaie de poursuivre car ta dernière question me semble floue...
L'énoncé ne te donne pas $U_0$ ...

@mtschoon si U0=a

@hugopep87 , sans formulation rigoureuse de toutes les données de la question, ce n'est pas possible de répondre.

Il faut avoir des précisions sur $a$ (son signe par exemple)

@mtschoon désolé

@hugopep87 mais j’ai une autre question je dois démontrer par recurence que Un>=a+n*g(a)
Et je n’y arrive pas

Quelqu’un peut il m’aider ??

@hugopep87

Quelles sont les différentes étapes d'une démonstration par récurrence ?

@Noemi l'initialisation puis l'hérédité

@hugopep87

Fais l'initialisation.

@Noemi je l'ai faite mais czts après que je bloque

@Noemi j'ai aussi fait la phrase entre les deux étapes

@hugopep87

Tu supposes la propriété vraie à l'ordre $k$ et tu démontres que :
$uk+1≥a+(k+1)×g(a)u_{k+1} \geq a+(k+1)\times g(a)$

@Noemi oui mais après ça je ne comprends pas quoi faire

@Noemi j'ai essayer de faire qqchose mais le résultat est complètement faux

@hugopep87

Indique tes calculs.

@Noemi je suis partie de Un et j'ai fait des calculs pour avoir Un+1 et j'ai fait les mêmes calculs de l'autre côté et ça donne Un+1=a+n+g(a)+exp(2)-exp(Un)

@hugopep87

Utilise la relation :
$u_{k+1}-u_k=g(u_k) et le fait que la suite est croissante.

@Noemi je ne comprends vraiment pas la

@hugopep87

$uk≥a+k×g(a)u_{k} \geq a+k\times g(a)$
$u_{k+1}=u_k+g(u_k)$
Donc
$uk+1≥....u_{k+1}\geq ....$

En utilisant les variation de la fonction $g$
....

Conclusion

$uk+1≥a+(k+1)×g(a)u_{k+1} \geq a+(k+1)\times g(a)$

@Noemi honnêtement la je suis perdu je n'arrive pas à comprendre la où vous voulez allez

@hugopep87

J'ai indiqué les calculs, il reste à compléter les pointillés.
Consulte l'ensemble de l'aide que tu as obtenu et indique les points que tu n'as pas compris.
je me déconnecte.

@Noemi merci même si je reste bloquée car je ne comprends pas

@hugopep87

Visiblement tu fais peu d'effort :
$uk≥a+k×g(a)u_k \geq a+k\times g(a)$
Comme $u_{k+1}=u_k+g(u_k)$ on déduit :
$uk+1≥a+k×g(a)+g(uk)u_{k+1}\geq a + k\times g(a)+g(u_k)$
La suite $u_n)$ est croissante donc $g(uk)>g(a)g(u_k) \gt g(a)$
Donc
$uk+1≥a+k×g(a)+g(a)u_{k+1}\geq a + k\times g(a)+g(a)$

Conclusion
.....