affixe du point M avec z

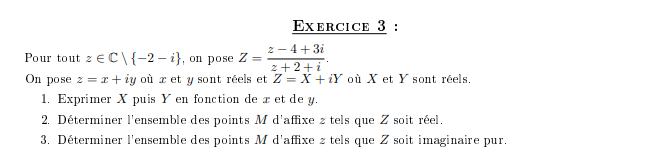
Bonjour je ne comprend pas l'exercice est ce que quel qu'un pourrait m'aider s'il vous plait .

Le scan de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques figures sont autorisés.

Ecris l'énoncé, indique tes éléments de réponse et tu obtiendras des pistes de résolution.

Le scan va être supprimé.

@Noemi ah je savais pas donc mon ennocé c'est:
pour tout z complexe sauf -2-i , on pose Z=(z-4+3i)/(z+2+i)
on pose z=x+iy avec x et y réels et Z=X+iY avec X et Y réels
1)Exprimer X puis Y en fonction de x et de y

@Luukao-_

Indique tes calculs.

@Noemi Le probleme c'est que je ne sais pas comment commencée mes calculs

@Luukao-_
Tu remplaces $z$ par $x + i y$
soit :
$z - 4 + 3 i = x + i y - 4 + 3 i = x - 4 + i (3 + y)$
fait le calcul pour le dénominateur :
$z + 2 + i = . . .$

@Noemi cela fait : x+2+i(1+y)

@Luukao-_

Donc $\dfrac{x-4+i(3+y)}{x+2+i(1+y)}$
Il faut rendre le dénominateur réel donc multiplier numérateur et dénominateur par l'expression conjuguée du dénominateur.
Calcule :
$[x + 2 + i (1 + y)] [x + 2 - i (1 + y)] = . . .$
puis le numérateur

@Noemi cela donne (x+2)² + (y+1)²

@Luukao-_ si j'étant tout mon calcul je trouve
x²-2x-5-4y-y²+i(2x+6y+10)
/
(x+2)²+(1+y)²

@Luukao-_

Calcule :
$[x - 4 + i (3 + y)] [x + 2 - i (1 + y)] = . . .$

@Noemi c'est bon normalement j'ai réussi est ce que vous pouvez juste me dire si j'ai les bons résultats?
Q1=X=x²-2x-5+4y+y²/(x+2)²+(1+y)²
Y=2x+6y+10/(x+2)²+(1+y)²
Q2)l'ensemble est une droite d'équation y=-2x-10/6

Q3)l'ensemble est un cercle de centre a(1;-2) et de rayon racine de 10

la question 2 et 3 c'est déterminer l'ensemble des points d'affixe z tel que Z soit réel (q1) ou imaginaire (q2)
merci

@Luukao-_

Refais le calcul que j'ai indiqué.

@Noemi x²-x-5+5i(1+y)+2y+y² je pense que c'est ça

@Luukao-_

Tu dois trouver : $x^2-2x-5+4y+y^2+2i(x+3y+5)$
Tu peux en déduire : $X$ et $Y$ .

@Noemi donc après je dois faire quoi ?

@Noemi X=x²-x-5
Y=5(1+y)+2y+y²
je pense

@Luukao-_
$X$ correspond à la partie réelle :
$\dfrac{x^2-2x-5+y^2+4y}{(x+2)^2+(1+y)^2}$
$Y$ correspond à la partie imaginaire :
$Y = . . .$

@Noemi 5(1+y)/(x+2)²+(1+y)²

@Luukao-_

Partie imaginaire : $Y = 2 (x + 3 y + 5)$
Question 2, tu cherches l'ensemble des points tel que $x + 3 y + 5 = 0$ .

Question 3, Tu cherches l'ensemble des points tel que $x^2-2x-5+y^2+4y=0$ .

@Noemi on a y=1

@Luukao-_
2. Non $x + 3 y + 5$ qui est l'équation d'une .....
que tu peux écrire sous forme réduite $y = . . . .$

@Noemi l'equation d'une drooite

@Luukao-_

Oui équation d'une droite.
Passe à la question 3 en factorisant.

@Noemi j'arrive pas a factoriser les x

@Luukao-_

Il faut utiliser les identités remarquables.
$x-1)^2-1-5+(y+2)^2-4= 0$
soit
$x-1)^2+(y+2)^2= 10$
qui correspond à l'équation d'un ....

@Noemi cercle ?

@Luukao-_

Oui cercle de centre $(1; - 2)$ et de rayon $10\sqrt{10}$ .

merci beaucoup pour votre aide

@Luukao-_

C'est très bien, tu as suivi les conseils et réalisé les calculs demandés. J'espère que tu as compris le raisonnement.

@Noemi il y a une faute au début nan on dit que Z=x-4+i(3+y) et après on résoud x-3+i(1+y)

@Luukao-_

Exact, j'ai rectifié les calculs. Vérifie l'ensemble des réponses.