Limite de fonction, courbe
-
Ddricce2906 dernière édition par
Soit f la fonction définie sur R
par f(x) = √x^2/x^2+1
et sa courbe représentative C dans un repère d'origine O- Justifier que f est dérivable sur ]-∞; O[ et sur ]0; +infini[.
- a. Démontrer que le taux d'accroissement de la fonction f entre 0 et 0 + h est : r (h) =
|h|/h√ 1/h^2+1 où h ≠ 0.
b. Calculer la limite de r(h) en 0 à droite. On note cette limite f’d(0) et on dit que f est dérivable en 0 à droite.
c. Calculer la limite de r(h) en 0 à gauche. On note cette limite f'g(0) et on dit que f est dérivable en 0 à gauche. - La fonction f est dérivable en O si f’d(0) = f’g(0).
La fonction f est-elle dérivable en 0? - La courbe C admet au point O deux demi-tangentes de coefficients directeurs respectifs f’d(0) et f’g(0).
Tracer dans un repère la courbe C et ses deux demi-tangentes en O.
svp j’ai besoin d’aide pour cet exo, c’est un dm a rendre mais je ne comprends pas !
PS: c’est une grande racine qui s’applique sur toute la division,
HELPP PLEASEEE
-
mtschoon dernière édition par mtschoon

@julie1201 , bonjour,
Ici, la politesse n'est pas une option.De plus, le multi-postage n'est pas autorisé.
Je te mets un lien sur les consignes avant de poster
https://forum.mathforu.com/topic/1383/stop-lire-ce-sujet-tu-devras-avant-de-poster-ton-message
-
mtschoon dernière édition par mtschoon

@julie1201 ,
Vu que tu n'utilises pas le Latex, il faut mettre des parenthèses pour que tes formules soient compréhensibles.
Je suppose (?) que f(x)=x2x2+1f(x)=\sqrt{\dfrac{x^2}{x^2+1}}f(x)=x2+1x2
Quelques pistes,
1 ) La fonction xxx-> x2x2+1\dfrac{x^2}{x^2+1}x2+1x2 est définie et dérivable sur RRR comme quotient de deux fonctions définies et dérivables sur RRR (avec dénominateur non nul)
Par contre la fonction XXX-> X\sqrt XX est définie pour X≥0X\ge 0X≥0 et dérivable pour X>0X\gt0X>0
Ici : X=x2x2+1X=\dfrac{x^2}{x^2+1}X=x2+1x2
Pour tout x réel, on a bien X≥0X\ge 0X≥0
Par contre pour la dérivabilité X>0X\gt 0X>0 <=> x≠0x\ne 0x=0
Conclusion :
fff est définie sur R
fff est dérivable sur ]−∞,0[]-\infty,0[]−∞,0[ et sur ]0,+∞[]0,+\infty[]0,+∞[
-
mtschoon dernière édition par mtschoon

Pour la 2), je ne comprends pas ce que tu as écrit pour le taux d'accroissement r(h)r(h)r(h) de la fonction f
Je le calcule.
A toi de voir si ça correspond à ton énoncé.
r(h)=f(h)−f(0)hr(h)=\dfrac{f(h)-f(0)}{h}r(h)=hf(h)−f(0)f(0)=0f(0)=0f(0)=0 donc :
r(h)=f(h)h=h2h2+1×1hr(h)=\dfrac{f(h)}{h}=\sqrt{\dfrac{h^2}{h^2+1}}\times \dfrac{1}{h}r(h)=hf(h)=h2+1h2×h1
r(h)=h2h2+1×1hr(h)=\dfrac{\sqrt{h^2}}{\sqrt{h^2+1}}\times \dfrac{1}{h}r(h)=h2+1h2×h1
Or, h2=∣h∣\sqrt{h^2}=|h|h2=∣h∣
Donc :
r(h)=∣h∣h2+1×1hr(h)=\dfrac{|h|}{\sqrt{h^2+1}}\times \dfrac{1}{h}r(h)=h2+1∣h∣×h1
f(h)=∣h∣h×1h2+1\boxed{f(h)= \dfrac{|h|}{h}\times \dfrac{1}{\sqrt{h^2+1}}}f(h)=h∣h∣×h2+11
Je te laisse poursuivre pour trouver les limites à droite et à gauche de 0 et les déductions pour la dérivabilité en 0.
Donne tes réponses si tu veux aide et/ou vérification.
-
Ddricce2906 dernière édition par
@mtschoon
Excusez moi mais je n’arrivais pas à retrouver mon post donc j’ai reposé ma question et oui je suis nouvelle donc je ne m’y connais pas forcément.
-
Ddricce2906 dernière édition par
Merci pour ces reponses !
j’ai aussi fait les questions des limites a gauche et a droite mais aucune idee si c’est bon ou pas :r(0)= √(1/0^2+1) = 1
soit
f’d(0)= 1r(0)= √(1/0^2+1) = 1
soit f’g(0)=1donc f’d(0)=f’g(0)
F est donc dérivable en 0
-
BBlack-Jack dernière édition par
@dricce2906 a dit dans Limite de fonction, courbe :
Merci pour ces reponses !
j’ai aussi fait les questions des limites a gauche et a droite mais aucune idee si c’est bon ou pas :r(0)= √(1/0^2+1) = 1
soit
f’d(0)= 1r(0)= √(1/0^2+1) = 1
soit f’g(0)=1donc f’d(0)=f’g(0)
F est donc dérivable en 0
Bonjour,
Il y a une erreur. la lim pour x --> 0- du taux d'accroissement est -1 et pas +1
-
Ddricce2906 dernière édition par
@Black-Jack
Comment ça ? sur ma calculatrice j’obtiens 1 et non -1
-
BBlack-Jack dernière édition par Black-Jack
@dricce2906 a dit dans Limite de fonction, courbe :
@Black-Jack
Comment ça ? sur ma calculatrice j’obtiens 1 et non -1C'est que tu utilises mal ta calculette.
f(h)=∣h∣h×1h2+1f(h) = \frac{|h|}{h} \times \frac{1}{ \sqrt{h^2 + 1}}f(h)=h∣h∣×h2+11
Pour h --> 0- (donc très près de zéro MAIS négatif)
Essaie par exemple avec h = -0,0001, il vient
f(h)=∣h∣h×1h2+1f(h) = \frac{|h|}{h} \times \frac{1}{ \sqrt{h^2 + 1}}f(h)=h∣h∣×h2+11
f(−0,0001)=∣−0,001∣−0,001×10,0012+1f(-0,0001) = \frac{|-0,001|}{-0,001} \times \frac{1}{\sqrt{0,001^2 + 1}}f(−0,0001)=−0,001∣−0,001∣×0,0012+11
f(−0,0001)=0,001−0,001×10,0012+1f(-0,0001) = \frac{0,001}{-0,001} \times \frac{1}{\sqrt{0,001^2 + 1}}f(−0,0001)=−0,0010,001×0,0012+11
f(−0,0001)=−1×11,000001f(-0,0001) = -1 \times \frac{1}{\sqrt{1,000001}}f(−0,0001)=−1×1,0000011
f(−0,0001)=−0,9999995f(-0,0001) = -0,9999995f(−0,0001)=−0,9999995Penses-tu encore que pour h --> 0- , f(h) tend vers 1 ou bien plutôt vers -1 ?
-
Ddricce2906 dernière édition par
@Black-Jack
Mais pourtant je dois remplacer h par 0 donc ça fait : r(0)= 0/0 x 1/√0^2+1j’obtiens « erreur syntaxe »
je crois que c’est les doubles barres de h que je ne comprends pas
 pourtant c’est bien valeur absolue? comment le faire sur la calculatrice ?
pourtant c’est bien valeur absolue? comment le faire sur la calculatrice ?Merci
-
BBlack-Jack dernière édition par
@dricce2906 a dit dans Limite de fonction, courbe :
@Black-Jack
Mais pourtant je dois remplacer h par 0 donc ça fait : r(0)= 0/0 x 1/√0^2+1j’obtiens « erreur syntaxe »
je crois que c’est les doubles barres de h que je ne comprends pas
 pourtant c’est bien valeur absolue? comment le faire sur la calculatrice ?
pourtant c’est bien valeur absolue? comment le faire sur la calculatrice ?Merci
Non, il ne faut pas remplacer h par 0
|h| signifie "valeur absolue de h".
Si tu remplaces h par 0, alors |h| = 0 et h = 0 ... et dans l'expression de f(h), |h|/h est une division de zéro par zéro ... ce qui ne peut jamais se faire.
Pour voir ce qui se passe lorsque h s'approche de la valeur 0 (sans l'atteindre), il faut distinguer 2 cas.
a)
Si h s'approche de la valeur 0 (sans l'atteindre) en restant négatif, alors |h|/h s'approche de très près de la valeur -1 (il suffit d'essayer avec une valeur de h très proche de zéro mais négative) pour comprendre.Par exemple si h = -0,001 (donc près de zéro mais négatif), alors h = -0,001 et |h| = 0,001 et donc
|h|/h = 0,001/(-0,001) = -1
b)
Si h s'approche de la valeur 0 (sans l'atteindre) en restant positif, alors |h|/h s'approche de très près de la valeur +1 (il suffit d'essayer avec une valeur de h très proche de zéro mais positive) pour comprendre.Par exemple si h = 0,001 (donc près de zéro mais positif), alors h = 0,001 et |h| = 0,001 et donc
|h|/h = 0,001/0,001 = 1
Si tu ne comprends pas la signification des || entourant le h ... va voir dans ton cours (ou sur le net) la notion de "valeur absolue".
-
mtschoon dernière édition par

Bonsoir,
@dricce2906 , si tu connais mal la notion de valeur absolue, tu peux consulter la vidéo ici :
-
mtschoon dernière édition par

@dricce2906 , bonsoir,
J'espère que tu as pris le temps de consulter la vidéo.
Si je résume :
Pour h>0\boxed{h\gt 0}h>0 h2=∣h∣=h\sqrt{h^2}=|h|=hh2=∣h∣=h donc ∣h∣h=1\dfrac{|h|}{h}=1h∣h∣=1
Donc r(h)=1h2+1r(h)=\dfrac{1}{\sqrt{h^2+1}}r(h)=h2+11limh→0,h>0r(h)=102+1=1\displaystyle \lim_{h \to 0, h\gt 0}r(h)=\dfrac{1}{\sqrt{0^2+1}}=1h→0,h>0limr(h)=02+11=1
111 est le nombre dérivée à droite de fff en 000
Pour h<0\boxed{h\lt 0}h<0 h2=∣h∣=−h\sqrt{h^2}=|h|=-hh2=∣h∣=−h donc ∣h∣h=−1\dfrac{|h|}{h}=-1h∣h∣=−1
Donc r(h)=−1h2+1r(h)=-\dfrac{1}{\sqrt{h^2+1}}r(h)=−h2+11limh→0,h<0r(h)=−102+1=−1\displaystyle \lim_{h \to 0, h\lt 0}r(h)=-\dfrac{1}{\sqrt{0^2+1}}=-1h→0,h<0limr(h)=−02+11=−1
−1-1−1 est le nombre dérivée à gauche de fff en 000
−1≠1\boxed{-1\ne 1}−1=1 : tu tires la conclusion sur la non dérivabilité de fff en 0 (ça doit être dans ton cours)
−1-1−1 et 111 sont les coefficients directeurs respectifs des deux demi-tangentes à la représentation graphique defff en 000
Regarde tout ça de près et indique si c'est clair (ou non) pour toi.
-
Ddricce2906 dernière édition par
Merci beaucoup, oui j’ai pris le temps de regarder la video de Yvan Monka.
Je comprends mieux, merci.
En cours, on n’a jamais vu ca avec ma prof donc ca m’aide beaucoup.
je pense pouvoir tracer les 2 demies tangentes car celle qui a un coefficient directeur negatif descend, et l’autre monte. Je verrai bien si j’y arrive.Encore merci.
Julie
-
mtschoon dernière édition par

@dricce2906 , je te joins la représentation graphique.
Compare avec la tienne et demande si besoinLa courbe est en bleu
La demi-tangente à droite (Td)(T_d)(Td) au point O est en rouge.
La demi-tangente à gauche (Tg)(T_g)(Tg) au point O est en vert.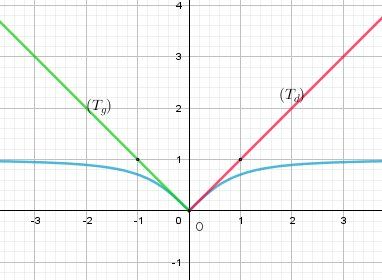
-
Ddricce2906 dernière édition par
Merci beaucoup, effectivement je l’avais faite sur ma calculatrice et j’obtiens aussi cette courbe.
Il ne me reste plus qu’à tracer mes demies tangentes.
Merci.
-
mtschoon dernière édition par

De rien @dricce2906 et bon DM !