maths: vecteurs, droite et plan dans l’espace

Bonjour, voici mon problème. Image PNG.png
Soit ABCDEFGH un cube , I un point du segment [AD] , J un point du segment [BC],
et K un point du segment [EF] tels que les droites (IJ) et (AB) ne sont pas parallèles.

Donner l'intersection des plans (IJK)
et (ABC). 2) En déduire l'intersection
des plans (IK) et (EFG). 3) Justifier que les droites (IJ) et (AB) sont sécantes . Déterminer ainsi
l'intersection des plans (IJK) et
(ABF) .
Déterminer et terminer ainsi la section
du cube ABCDEFGH par le plan (IJK)

Pouvez vous m’aider ?
Merci d’avance.

@lalie123, bonjour,

Si ça peut t'aider, je te joins un schéma complété.
Tous les éléments appartenant au plan (IJK) sont en rouge.

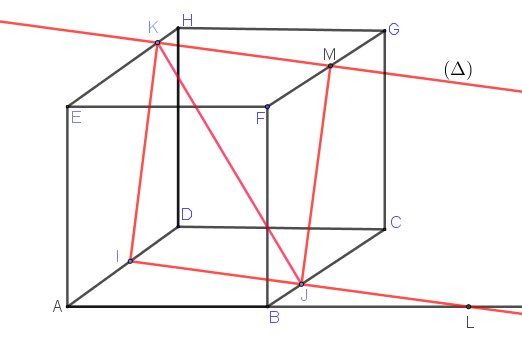
Quelques pistes pour démarrer,

1 ) L'intersection des plans (IJK) et (ABC) est la droite (IJ)
(à justifier)

2 ) Les plans (ABC) et (EFG) sont parallèles.
Tout plan qui coupe l'un coupe l'autre et les intersections sont des droites parallèles.
Soit $(Δ)(\Delta)$ la droite passant par $K$ et parallèle à la droite $(I J)$ .
Elle coupe $(F G)$ en $M$
L'intersection des plans $(I J K)$ et $(E F G)$ est cette droite $(Δ)(\Delta)$ c'est à dire $(K M)$

Je te laisse poursuivre.
Reposte si besoin.

@mtschoon
Mon schéma n’est pas très clair, mais le point k est placé entre E et F et non entre E et H.
J’admets que sur ma photo on croit voir un K, mais ce n’est pas le cas.
Du à ca, on ne peux pas tracer une parallèle car elle n’appartient plus au plan (EFG)

@lalie123 , OK
Je te joins un schéma avec $K$ sur le segment [EF]

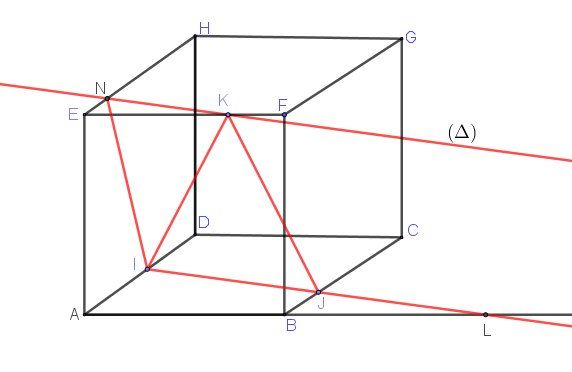
Le raisonnement est le même .
La droite $(Δ)(\Delta)$ passant par $K$ et parallèle à $(I J)$ coupe le segment $[E H]$ en $N$

@mtschoon
Merci pour votre réponse

De rien @lalie123

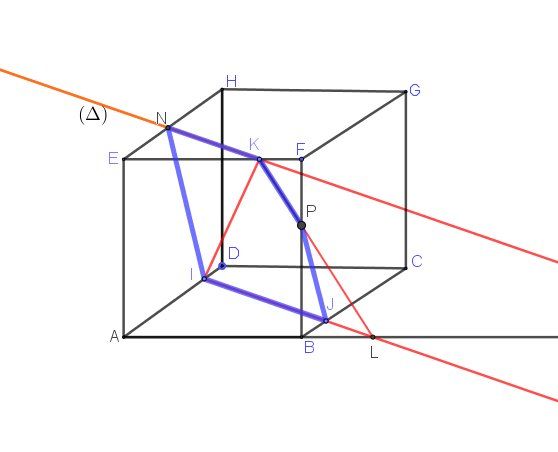
Si besoin, je t'indique la section du cube par le plan $(I J K)$ (en trait épais, bleu foncé) que tu dois trouver, après avoir complété avec le point P.