Expression fractionaire avec des racines carrées
-
LLey83 dernière édition par Noemi
Bonjour, bonsoir
Je suis en 2nd général. J'ai un DM de Math à faire et je n'arrive pas le dernier exercice, j'ai le résultat à la calculatrice qui est 3 mais je n'arrive pas à détaillé le calcul. La consigne est "Simplifier les expressions suivantes de façon astucieuse".C=3+53−5+3−53+5C=\sqrt{\dfrac{3+\sqrt5}{3-\sqrt5}}+ \sqrt{\dfrac{3-\sqrt5}{3+\sqrt5}}C=3−53+5+3+53−5
Merci beaucoup d'avance !
Bonne journée, soiréeRelation mise sous Latex par la modération du site.
-
Rend le dénominateur entier pour chacune des racines
3+53−5=(3+5)(3+5)(3−5)(3+5)=(3+5)24\dfrac{3+\sqrt5}{3-\sqrt5}=\dfrac{(3+\sqrt5)(3+\sqrt5)}{(3-\sqrt5)(3+\sqrt5)}= \dfrac{(3+\sqrt5)^2}{4}3−53+5=(3−5)(3+5)(3+5)(3+5)=4(3+5)2je te laisse poursuivre les calculs. Indique tes calculs et/ou résultats si tu souhaites une vérification.
-
LLey83 dernière édition par
@Noemi Merci beaucoup de m'avoir répondu !
Je sais pas si mon résultat est bon mais j'ai trouvé ceci :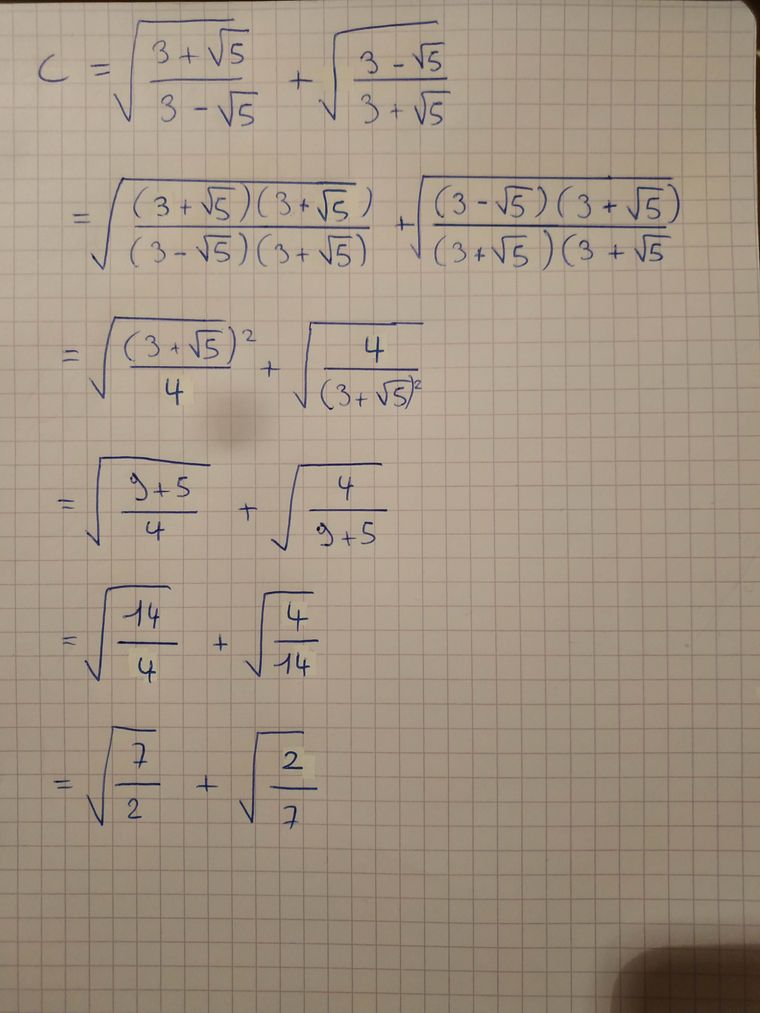
-
Attention : (3+5)2=9+65+5(3+\sqrt5)^2= 9 + 6\sqrt5+5(3+5)2=9+65+5
(3+5)24=3+52\sqrt{\dfrac{(3+\sqrt5)^2}{4}}=\dfrac{3+\sqrt5}{2}4(3+5)2=23+5
Pour le deuxième terme, tu dois écrire :
3−53+5=(3−5)(3−5)(3+5)(3−5)=(3−5)24\dfrac{3-\sqrt5}{3+\sqrt5}=\dfrac{(3-\sqrt5)(3-\sqrt5)}{(3+\sqrt5)(3-\sqrt5)}= \dfrac{(3-\sqrt5)^2}{4}3+53−5=(3+5)(3−5)(3−5)(3−5)=4(3−5)2Rectifie tes calculs
-
LLey83 dernière édition par
@Noemi Merci d'avoir répondu si vite !
J'ai corrigé mes erreurs et j'ai obtenu ceci :
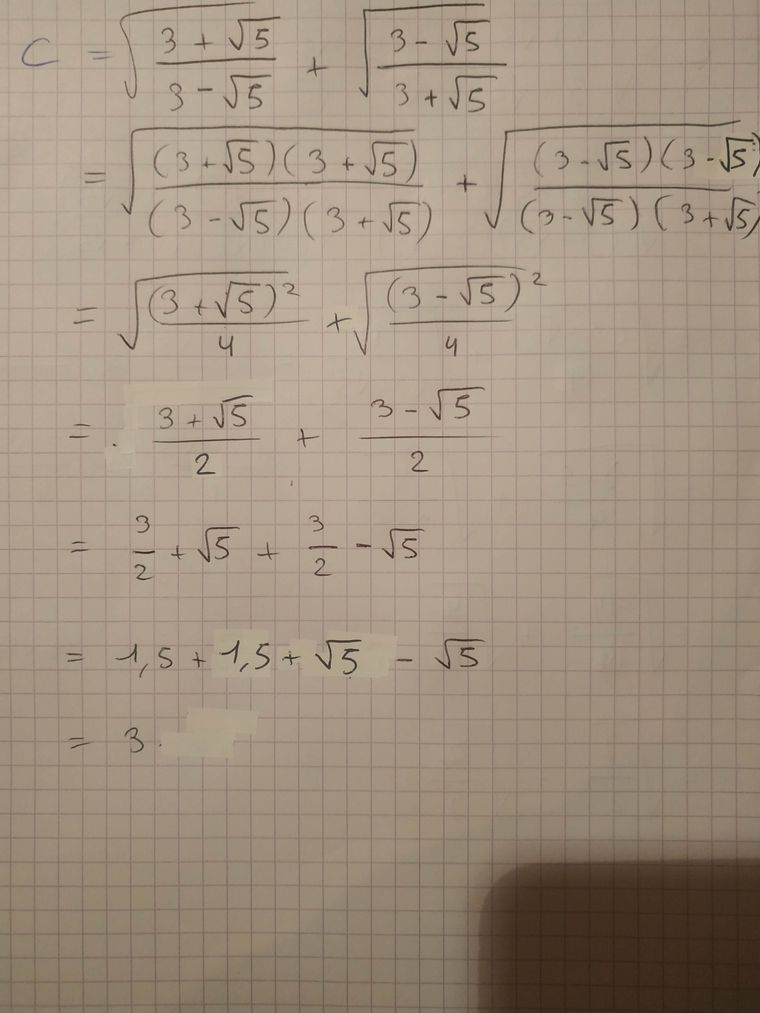
-
Attention, la fin est fausse.
3+52+3−52=3+5+3−52=62=...\dfrac{3+\sqrt5}{2}+ \dfrac{3-\sqrt5}{2}= \dfrac{3+\sqrt5+3-\sqrt5}{2}= \dfrac{6}{2}= ...23+5+23−5=23+5+3−5=26=...
-
LLey83 dernière édition par
@Noemi C'est bon j'ai réussi mon exercice ! Merci beaucoup pour tes réponses et merci pour le temps que tu m'as accordé.
Bonne soirée à toi !
-
Bonne soirée.