Etude de fonctions (signes de f'(x))

Bonsoir, j'ai encore pas mal de difficultés à réussir à trouver les variations d'une fonction, et j'aimerais bien comprendre avant mon prochain cours.

Par exemple, pour la fonction
$text alternatif$

le tableau de variations est le suivant:

Et je suis incapable de retrouver ceci pour les signes de f'(x).

Je sais que si f'(x) est négative (ce qui est le cas ici: $text alternatif$ , alors avant le 0 en abscisse son signe est positif puis négatif après le 0.

Mais ducoup ce cas m'embête car je suis tenté de mettre une + dans la première case. Je ne comprend pas comment déduire les signe de f'(x).

@leol Bonjour,

Vérifie le calcul pour la dérivée.
A quoi correspondent $x_1$ et $x_2$ ?
Si la dérivée est négative, le signe devrait être toujours - (moins).

@Noemi Bonjour,

Alors x1 = -1-√2
et x2 = 1-√2

Pour la dérivée, je l’ai revue plusieurs fois et je ne vois pas d’erreur.

@leol

La dérivée :
$\dfrac{2x(x^2-x)-(x^2+1)(2x-1)}{(x^2-x)^2}$

$f′(x)=2x3−2x2−2x3−2x+x2+1(x2−x)2=....f'(x)=\dfrac{2x^3-2x^2-2x^3-2x+x^2+1}{(x^2-x)^2}= ....$

@Noemi Et bien je trouve le même résultat qu’au dessus : -x^2 -2x -1 / (x^2 - x)^2, c’est une erreur ?

@leol

Une erreur de signe.

$f′(x)=2x3−2x2−2x3−2x+x2+1(x2−x)2=−x2−2x+1(x2−x)2f'(x)=\dfrac{2x^3-2x^2-2x^3-2x+x^2+1}{(x^2-x)^2}= \dfrac{-x^2-2x+1}{(x^2-x)^2}$

Bonjour,

@leol a dit dans Etude de fonctions (signes de f'(x)) :

Alors x1 = -1-√2
et x2 = 1-√2

J'espère @leol que tu as compris maintenant ton erreur de signes sur la dérivée (voir calcul ed Noemi)

Avec la dérivée exacte, tu dois trouver
$x1=−1−2x_1=-1-\sqrt 2$
$x2=−1+2x_2=-1+\sqrt 2$

Tout ceci est conforme au tableau de variation que tu as donné.

@mtschoon @Noemi d'accord merci je vais reprendre ça

Oui @leol
La meilleure façon est de refaire l'exercice seul pour être sûr de le maîtriser.
Bon travail!

Les variations de $f$ sur $I$ sont données par le signe de $f^{'}$ sur $I$ .
$ddx(x2+1x2−x)=−x2−2x+1(x2−x)2\dfrac{\text d}{\text dx}\left(\dfrac{x^2+1}{x^2-x} \right)=\dfrac{-x^2-2x+1}{(x^2-x)^2}$ .

$∀x∈R,(x2−x)2⩾0\forall x\in \mathbb{R},(x^2-x)^2\geqslant 0$ , le signe de $f^{'}$ ne dépend alors que du numérateur. Ses racines sont données par la formule quadratique $x=−b±b2−4ac2ax=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$ .
On trouve:
$x1=−1+2x_1=-1+\sqrt{2}$
$x2=−1−2x_2=-1-\sqrt{2}$

$f^{'}$ est du signe de $a=−1<0a=-1\lt 0$ à l'éxtérieur des racines.

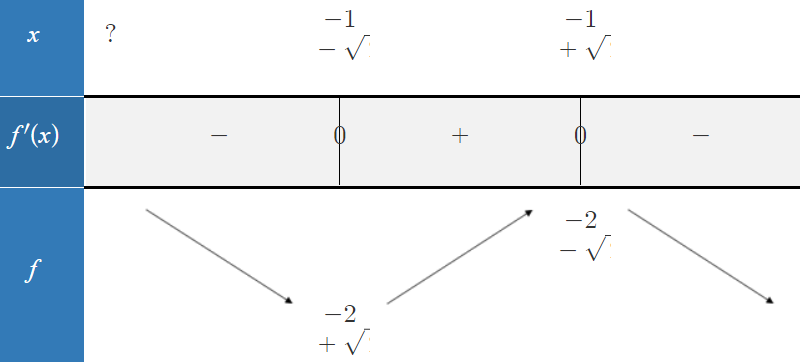
Où $−2+2-2+\sqrt{2}$ et $−2−2-2-\sqrt{2}$ sont les images respectives des deux racines par la fonction $f$ .

@............................, bonjour

Ici, la politesse n'est pas un option...
Il faudra y penser une autre fois.

Le tableau de variation que tu proposes est totalement faux, car tu ne tiens pas compte de l'ensemble de définition de $f$ qui est :
$D_f=R$ \ {0,1}

On ne peux pas diviser par 0.
La condition d'existence de f est :
$x2−x≠0x^2-x\ne 0$ <=> $x(x−1)≠0x(x-1)\ne 0$ <=> $x≠0x\ne 0$ et $x≠1x\ne 1$

La tableau de variation proposé par @leol est exact.
Va le consulter en haut de ce topic.

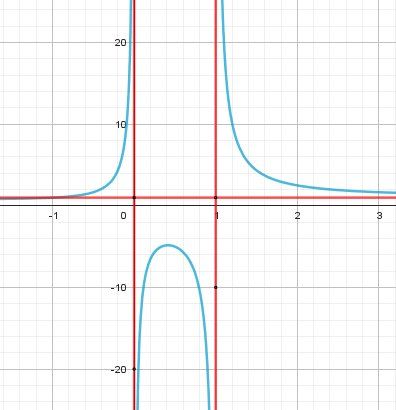
@...................... , tu peux aussi consulter la représentation graphique de $f$ (couleur bleu) avec ses 3 asymptotes (couleur rouge) d'équations :
$x = 0$ et $x = 1$ droites "verticales" correspondant aux valeurs "interdites"
$y = 1$ asymptôte horizontale lorsque $x$ tend vers $−∞-\infty$ et $+∞+\infty$

Bonsoir,

Comme je viens de constater que le "pseudo dérangeant" venait d'être remplacé par "Ancien Utilisateur", j'ai supprimé ce "pseudo dérangeant" par des ................, dans mes deux dernières réponses, par respect pour la personne dont le nom/prénom avait servi pseudo.

@mtschoon Merci à toi

C'est tout à fait normal @Casebas !