Exercice probabilité

[hiba_mrcnn]

Bonjour est-ce que quelqu’un pourrait m’aider

Dans une classe de 35 élèves, 18 élèves pratiquent un sport, 7 jouent d'un instrument de musique et 20 pratiquent l'une ou l'autre de ces deux activités.
On choisit un élève de la classe au hasard.
On note S l'évènement « l'élève pratique un sport » et M l'évènement « l'élève joue d'un instrument de musique ».

1. a) Calculer la probabilité de S, M et S U M.
   b) En déduire la probabilité que l'élève pratique à la fois un sport et joue d'un instrument de musique.
2. Calculer la probabilité que l'élève joue d'un instrument de musique sachant qu'il pratique un sport.
3. Calculer la probabilité que l'élève pratique un sport sachant qu'il joue d'un instrument de musique.

[Noemi]

@hiba_mrcnn Bonjour,

Indique tes éléments de réponse et la question qui te pose problème.
As-tu réalisé un diagramme de Venn ?

[hiba_mrcnn]

@Noemi
Non

[Noemi]

@hiba_mrcnn

Donc commence par en faire un.

[mtschoon]

Bonjour,

@hiba_mrcnn , si besoin, voici un diagramme de Venn

Disque C : ensemble des élèves de la classe

A l'intérieur de ce disque C :
Disque S (couleur rosée) : ensemble des élèves faisant du sport
Disque M (couleur bleutée) : ensemble des élèves faisant dela musique

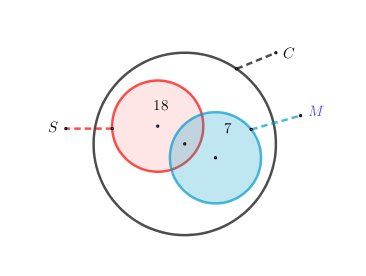
En appelant "cardinal" (abrévation : card) , le nombre d'éléments d'une partie, l'énoncé t'indique:
$card(C)=35$
$card(S)=18$
$card(M)=7$
$card(S\cup M)=20$

Regarde cela de près et réponds aux questions posées.
Tu peux donner tes réponses pour vérification si tu le souhaites.

[hiba_mrcnn]

Ce message a été supprimé !

[hiba_mrcnn]

@mtschoon

Questions

2)Calculer la probabilité que l'élève joue d'un instrument de musique sachant qu'il pratique un sport.
3) Calculer la probabilité que l'élève pratique un sport sachant qu'il joue d'un instrument de musique.

[hiba_mrcnn]

@mtschoon

Pouvez vous m’aider pour cet 2 questions svp

[mtschoon]

@hiba_mrcnn ,

Pour faire la 2) et la 3) il faut avoir trouvé les réponses de la 1)

Tu as dû trouver :

$p(S)=\frac{18}{35}$

$p(M)=\frac{7}{35}$

$p(S\cup M)=\frac{20}{35}$

$p(S\cap M)=p(S)+p(M)-p(S\cup M)=\frac{5}{35}$

Revois ton cours sur les probabilités conditonnelles si besoin.

2 ) $p_S(M)=\frac{p(M\cap S)}{p(S)}$ Tu comptes.

3 ) $p_M(S)=\frac{p(M\cap S)}{p(M)}$ Tu comptes.

[hiba_mrcnn]

@mtschoon

Oui
Et dcp
2) ps (M) = 20/35 sur 18/35
3) pm (S) = 5/35 sur 7/35 ?

[hiba_mrcnn]

@mtschoon

C’est équivaut à p( m) x p( s)

[mtschoon]

Bonjour,

@hiba_mrcnn a dit dans Exercice probabilité :

@mtschoon

Oui
Et dcp
2) ps (M) = 20/35 sur 18/35
3) pm (S) = 5/35 sur 7/35 ?

Ta réponse à la 2 ) est à revoir car tu confonds union et intersection.
Ta réponse à la 3 ) est bonne et tu peux la simplifier.

@hiba_mrcnn a dit dans Exercice probabilité :

@mtschoon
C’est équivaut à p( m) x p( s)

Non à cette remarque.