Problème extrêmement difficiles de trigo...

Bonjour, je bloque sur ces deux exercice de Trigo vraiment dur...., quelqu'un pour m'aider ? Merci d'avance !

ABCD est un quadrilatère avec ∠DAC = ∠CAB = 55°, ∠ACD = 15° et ∠BCA = 20°.
Calculer ∠ADB

Jule et Inès se trouvent à l'intersection de deux très longues avenues rectilignes formant entre elles un angle de 105°. Jule commence à marche le long de la première avenue à la vitesse de 4km/h alors que Inès s'élance sur la seconde d'un pas alerte : 6km/h. Sachant que leur téléphones ne peuvent être connectés que s'ils sont distants de moins de 16 km, pendant combien de temps nos deux personnages pourront-elles garder le contact?

@Julien34235 Bonjour,

Un seul exercice par post. Ouvre un autre sujet pour l'exercice 2.
Pour l'exercice 1, as-tu fait une figure ?

@Julien34235 a dit dans Problème extrêmement difficiles de trigo... :

Jule et Inès se trouvent à l'intersection de deux très longues avenues rectilignes formant entre elles un angle de 105°. Jule commence à marche le long de la première avenue à la vitesse de 4km/h alors que Inès s'élance sur la seconde d'un pas alerte : 6km/h. Sachant que leur téléphones ne peuvent être connectés que s'ils sont distants de moins de 16 km, pendant combien de temps nos deux personnages pourront-elles garder le contact?

Bonjour, je ne savais pas, désolé. Et oui, pour l'exercice un j'ai dessiné une figure

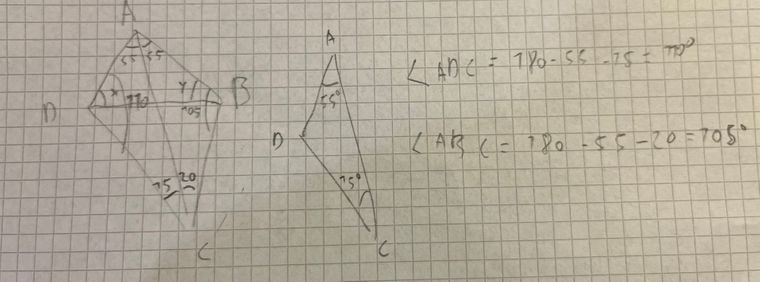
j'ai également fait des équations à 2 inconnues pour essayer de résoudre le problème mais ça m'arrive toujours à x+y = 70

par tatonement j'ai su que x=40 et que y=30 mais malgré le fait que le problème est résolu je ne crois pas avoir le droit d'utiliser une méthode par tatonement (à moins qu'il n'y a aucun autre moyen de savoir ?)

si vous voulez mon raisonnement

@Julien34235

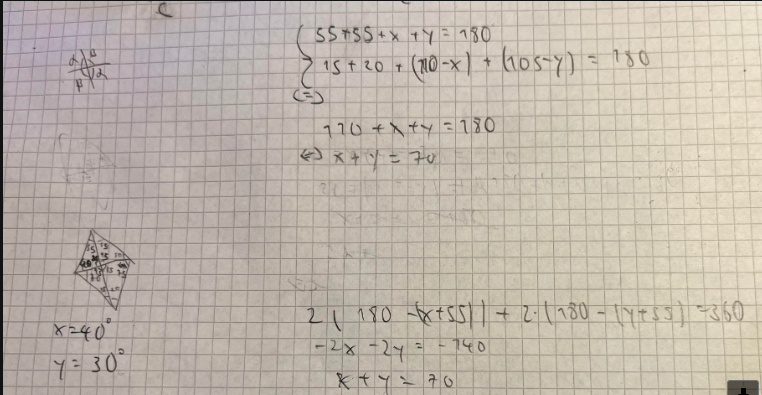
L'énoncé est-il complet ?

Bonjour, oui il l'est.

@Julien34235

Utilise la relation des sinus et celle d'Al kashi.

Bonsoir,
@Julien34235 , je reste perplexe sur l'exercice 1...!
Seulement quelques réflexions.

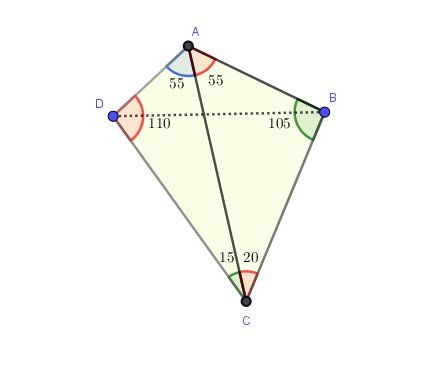
@Julien34235 , je suis d'acccord avec toi, en mettant en équations toutes les égalités d'angles possibles ( en utilisant le fait que la somme des angles de tout triangle vaut 180° ) on tombe sur des systèmes indéterminés.
J'ai même essayé en utilisant le point intersection des diagonales, idem : indétermination.
Faire des calculs avec les angles seuls ne suffit pas pour aboutir.

Comme te l'indique Noemi, la seule façon serait d'utiliser des propriétés relatives aux angles/cotés dans les triangles.
Mais, l'énoncé ne te donne rien sur les côtés...
Un seul côté suffirait d'ailleurs.

Tout triangle peut être défini par un côté connu compris entre deux angles connus.

Dans les triangles $A B C$ et $A D C$ , les angles de sommets A et C sont connus.
En connaissant $A C$ , tout s'éclairerait.
Il serait possible de calculer $A D$ , $A C$ (avec les sinus), puis $D B$ (avec Al-Kashi) puis le sinus de l'angle $ADB^\widehat{ADB}$ puis une valeur (approchée) de $ADB^\widehat{ADB}$

Alors, que dire...
ou bien revois ton énoncé pour savoir s'il ne donnerait pas la mesure de $A C$
ou bien demande à ton professeur s'il n'y a pas un oubli
ou bien prend une mesure de ton choix de $A C$ pour faire les calculs.
Dans ce cas , il faut indiquer que la mesure de $A C$ n'a pas d'influence sur la conclusion à trouver.
En changeant la mesure de $A C$ toutes les mesures de côtés changent ( la figure reste"semblable" , elle devient plus grande ou plus petite) mais les angles sont conservés.

Vois ce que tu peux faire ...

Je trouve que des indications sur la démarche aurait dû être données, surtout en Seconde.