Variation de fonction associée

Bonsoir. J'ai un exercice sur les variations des fonctions associé mais je n'arrive pas à faire.
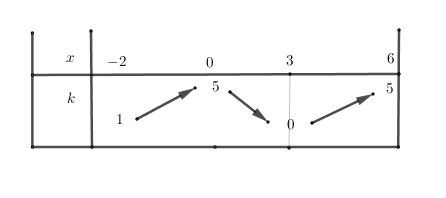
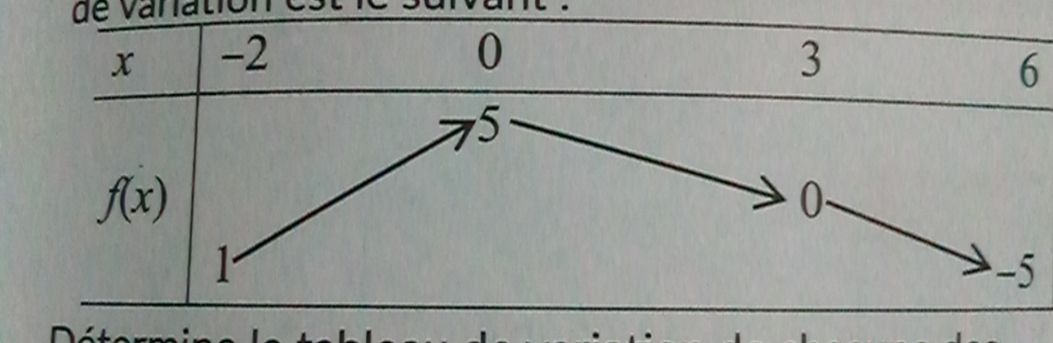
Soit f la fonction définie sur [-2;6] dont le tableau de variation.
Détermine le tableau de variation des fonctions: g: qui à x on associe f(x+1)-2; h: qui à x on associe -f(-x) et k: qui à x on associe|f(x)|

@Maxime-174 Bonjour,

Indique tes éléments de réponse et le cas qui te pose problème.

@Noemi bonjour
Je sais que la cour de g se déduit de celle de f par la translation du vecteur ū(-1;-2) et celle de h par la symétrie centrale

@Maxime-174

Donc applique ces éléments.
Pour $g$
$x$ ....
$g (x)$

@Noemi
Donc je dois construire la courbe de f puis celle de g et k et déduis leurs variation ?

@Maxime-174

La question que tu as indiqué est de déterminer le tableau de variation,
donc
$x$ ; -3 ; -1 ; ....
$g (x)$ ; -1 ; 3 ; ....

Bonjour,

@Maxime-174, j'espère que tu as compris la démarche.

Si besoin, un petit complément pour $g$

On passe de $C_f$ à $C_g$ par translation,
Les sens de variation sont conservés.
Tout point $M (x, y)$ de $C_f)$ a pour image un point $M^{'} (x^{'}, y^{'})$ de $C_g)$ tel que $MM′→=U→\overrightarrow{MM'}=\overrightarrow{U}$

$x^{'} - x = - 1$ donc $x^{'} = x - 1$
$y^{'} - y = - 2$ donc $y^{'} = y - 2$

Tu cherches les coordonnées des images $A^{'}, B^{'}, C^{'}, D^{'}$ des points $A (- 2, 1), B (0, 5), C (3, 0), (D (6, - 5)$

Sauf erreur, tu dois trouver le tableau de variation ainsi :

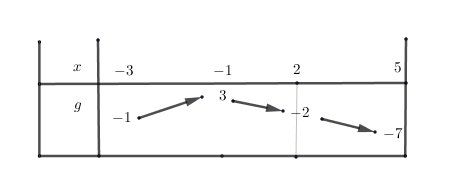
Essaie de poursuivre et donne tes réponses si tu souhaites une vérification

@Noemi bonsoir
J'ai du mal à vous comprendre quand vous dites x;-3;-1 et g(x);-1;3

@Maxime-174

Regarde la réponse de mtschoon.

Bonjour,

@Maxime-174 , Noemi t'a mis sur la voie de la démarche que j'ai essayé d'expliciter ensuite ( à relire si besoin ) .

@Noemi a dit dans Variation de fonction associée :

@Maxime-174
La question que tu as indiqué est de déterminer le tableau de variation,
donc
$x$ ; -3 ; -1 ; ....
$g (x)$ ; -1 ; 3 ; ....

cela veut dire que :
pour $x = - 3$ , $g (x) = - 1$
pour $x = - 1$ , $g (x) = 3$

@Noemi bonjour
Pour -f(-x) je dois appliquer la même méthode

@mtschoon bonjour
Pour k(x)=-f(-x) . Comme ils sont symétriques part rapport au centre alors leur sens de variation seront opposé

@Maxime-174

Que veux-tu dire par sens de variation opposé ?
Pour $k (x) = - f (- x)$
Recherche les valeurs de $k (- 6)$ , $k (- 3)$ , $k (0)$ et $k (2)$ puis dresse le tableau de variations.

@Noemi bonjour
J'aimerais vous demandez si vous avez choisi ces nombres arbitrairement ou si vous avez procédé à un calcul pour les trouver .

@Maxime-174

C'est la symétrie centrale : $OM′→=−OM→\overrightarrow{OM'}= -\overrightarrow{OM}$
donc je choisis $x^{'} = - x$ valeurs de $x$ du tableau de variation.

@Noemi
Je comprends maintenant

@Maxime-174

Parfait, tu peux dresser le tableau de variations.

@Noemi
Voici le tableau de variation que j'ai obtenu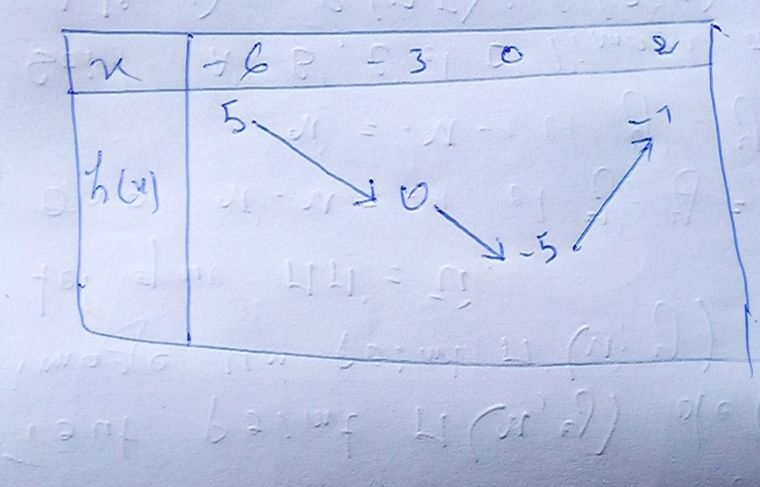 IMG_20221210_133345_457~2.jpg

@Maxime-174 , si tu parles de $h (x) = - f (- x)$ ( car dans l'énoncé tu as mis $h$ et dans le topic parfois c'est $k$ ...), c'est bon.

Tu peux passer $k (x) = ∣ f (x) ∣$

Si tu veux une synthèse générale sur les fonctions associées, tu peux regarder ici http://www.matheatre.fr/Maths/Ana/Docs/Ma_Ana_fonctions-associees.pdf

@mtschoon bonsoir
Pour la dernière question Toutes les parties du tableau de variations resteront inchangées lorsque les valeurs de f sont positives, et seront « inversées » lorsque les valeurs de f seront négatives.

@Maxime-174

C'est correct. Tu peux construire le tableau de variations.

@Maxime-174 , pour vérification éventuelle.

Bon travail.