démontrer qu'un vecteur est normal à un plan

Bonjour à vous tous,
j'envoi ce message car il y a un exercice sur lequel j'étais bloqué(je pense que j'ai trouvé les solutions). " voir le dessin ci-dessous en 3D"
Est ce que quelqu'un pourrai m'aider s'il vous plait?
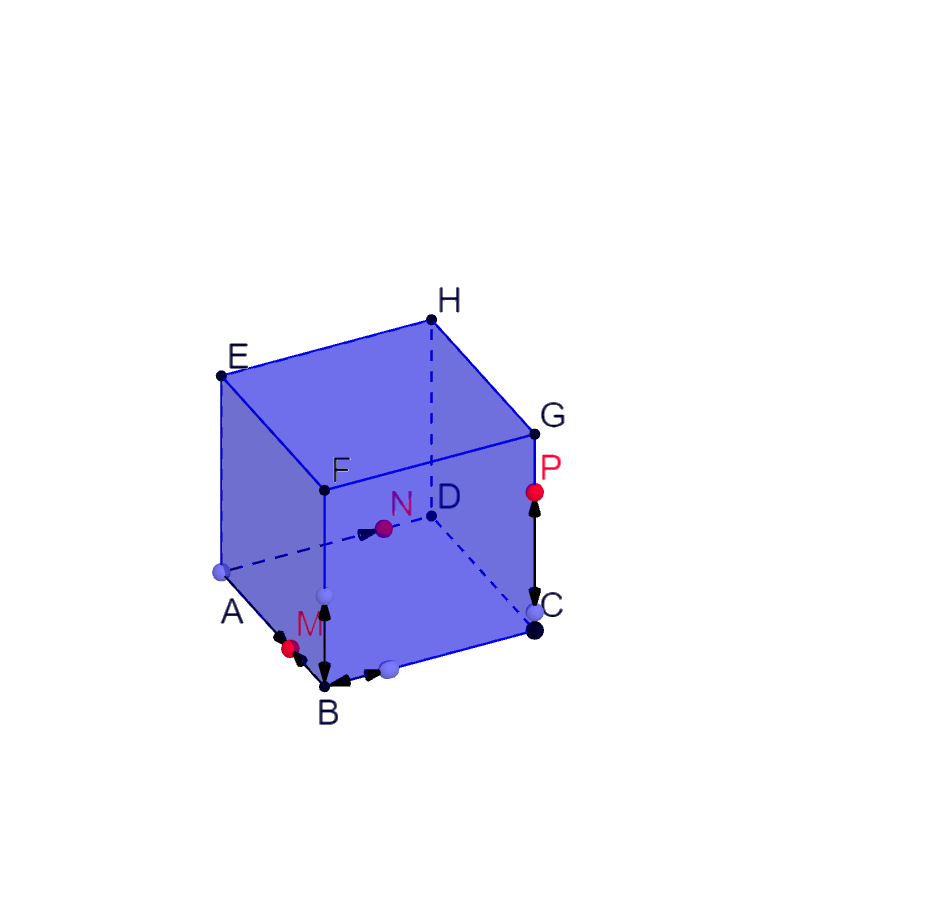
Voici l'énoncé: Dans un cube ABCDEFGH, les points M,N,P sont définis par AM=2/3.AB (ce sont des vecteurs)
AN = 2/3AD et CP =2/3 CG (vecteurs partout)
On choisit le repère (B,BA,BC,BF)
1)Démontrer que le vecteur AP est normal au plan (EMN).
2)En déduire une équation cartésienne du plan (EMN).

Voici mes réponses:
Méthode 1)+ simple : je calcul le produit scalaire de vecteur AP.EM et AP.MN( ou AP.EN je pense) ce qui doit donner 0 pour que le vecteur AP soit orthogonal avec le plan (EMN).
dans ce cube les coordonnées des points sont :
A(1,0,0) B(0,0,0) , C(0,1,0), D(1,1,0), F(0,0,1) ,E(1,0,1) G(0,1,1), H(1,1,1) M(1/3,0,0), N(1,2/3,0) P(0,1,2/3), . Et les coordonnées du vecteurs AP sont AP(-1,1,2/3).
Ensuite les deux vecteurs directeurs de EMN sont EM et EN .
EM(-2/3,0,-1) et EN(0,2/3,-1).

AP.EM= (2/3)-(2/3) =.0
AP.MN=(-1,1,2/3).(2/3,2/3,0) =0
AP.EN "même si c'est pas nécessaire" = 0.

Méthode 2 + compliqué
dans ce cube les coordonnées des points sont :
A(1,0,0) B(0,0,0) , C(0,1,0), D(1,1,0), F(0,0,1) ,E(1,0,1) G(0,1,1), H(1,1,1) M(1/3,0,0), N(1,2/3,0) P(0,1,2/3), . Et les coordonnées du vecteurs AP sont AP(-1,1,2/3).
Ensuite les deux vecteurs directeurs de EMN sont EM et EN .
EM(-2/3,0,-1) et EN(0,2/3,-1).
Le produit vectoriel (EM ^EN) donne le vecteur normal n( 2/3,-2/3,-4/9) = n
n= 1/3.AP ces deux vecteurs sont donc colinéaires. par conséquent AP est un vecteur orthogonal au plan (EMN).
Ensuite l'équation cartésienne du plan dépend du vecteur normal n je pense.
Cube definition patron diagonales .png

@Marvin , bonjour,

Pour la 1), effectivement , ce n'est pas nécessaire de calculer le produit scalaire $AP→.EN→\overrightarrow{AP}.\overrightarrow{EN}$ car un vecteur est normal à un plan si et seulement si il est orthogonal à 2 vecteurs non colinéaires de ce plan.

Remarque : vérifie tes calculs car je ne les ai pas vérifiés

Pour la 2), tu a déjà les coordonnées d'un vecteur normal $AP→\overrightarrow{AP}$

En appelant $(a, b, c)$ les coordonnées de ce vecteur normal, l'équation du plan $(E M N)$ est de la forme $a x + b y + c z + d = 0$

Pour trouver la valeur de $d$ , utilise les coordonnées d'un point du plan (ou E ou M ou N )

Remarque , si tu préfères, tu peux aussi utiliser le produit scalaire.
Soit R(x,y,z) un point quelconque du plan (EMN)
$AP→.ER→=0\overrightarrow{AP}.\overrightarrow{ER}=0$

Si tes calculs de la 1) sont bons, tu dois trouver :
$−x+y+23z+13=0-x+y+\dfrac{2}{3}z+\dfrac{1}{3}=0$ que tu peux transformer si tu le souhaites.

Bonjour @mtschoon ,

Oui j'ai vérifié mes calculs plusieurs fois justement car au début j'avais pas trouvé un produit scalaire nul.
Maintenant il n'y a pas d'erreur normalement.
Merci beaucoup pour ton aide, j'avais oublié certaines propriétés et ça fait perdre du temps

@Marvin ,

C'est sûr, il vaut mieux maîtriser le cours avant de faire les exercices , mais si maintenant tout est clair pour toi, c'est parfait !