Besoin d'aide sur un un devoir à rendre : exercice de géométrie
-
NNadia-matheuse dernière édition par Noemi
Bonjour,
J'ai besoin de votre aide pour résoudre 2 questions de géométrie d'un devoir maison. Je suis en 1ère spé maths/svt.
Un triangle ABC rectangle en A est tel que AB = 8 cm et AC = 4 cm. M est un point variable du segment (AB) et on pose AM = x cm. On considère le triangle équilatéral MBK de hauteur [KH] avec K et C de part et d'autre de la droite [AB]. On souhaite montrer qu'il existe une position de M telle que CM = KH et préciser si, dans cette position, les points C, M et K sont alignés ou pas. (Utiliser le théorème de Pythagore) :
-
Calculer CM² dans le triangle ACM - ok répondu
-
Calculer KH² dans le triangle KHM - ok répondu
-
Trouver l'équation avec : CM²= KH² et résoudre (je bloque)
-
Pour l'alignement des points : travailler tel que l'angle CMA = BMK = 60° (angles opposés par le sommet) (je bloque).
Je n'arrive pas à trouver la mesure KH². Pouvez-vous me donner la méthode à utiliser svp.
Merci beaucoup pour votre aide.
Bonne fin de journée et bon réveillon!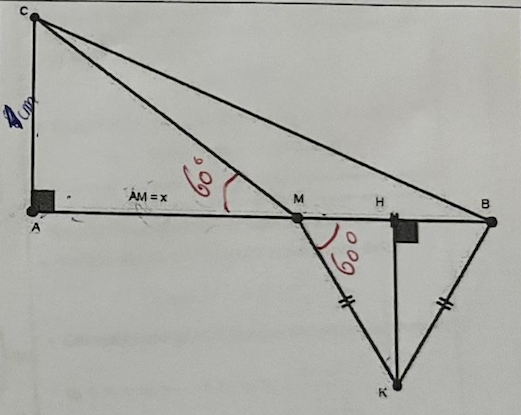
-
-
@Nadia-matheuse Bonjour,
Pour la question 3, il faut utiliser les résultats des questions 1 et 2.
Quelle réponse as-tu trouvée aux questions 1 et 2 ?
-
NNadia-matheuse dernière édition par
Bonsoir,
Merci pour votre retour rapide.
Voici mes réponses pour les questions 1 et 2 :
- On sait que ACM est un triangle rectangle en A, on utilise donc le théorème de pythagore.
CM² = AC² + AM²
CM² = 4²+ X²
CM = 16²+ X²- On sait que KAM est un triangle rectangle en H, on utilise donc le théorème de pythagore.
KH² = MK² - MH²
KH² = 4² - (8² - x / 2)
KH² = 26 - (64 - 16x + x² / 4)On remarque que MK + KB = AB donc MK étant la moitié de AB est égal à 4 cm.
Cela vous semble correct.
Merci pour votre aide.
-
La question 1. est juste à condition d'enlever le carré à 16 qui doit être sur CMCMCM.
CM2=16+x2CM^2=16+x^2CM2=16+x2Pour la question 2,
KH2=MK2+MH2KH^2=MK^2+MH^2KH2=MK2+MH2
or MK=MB=8−xMK=MB=8-xMK=MB=8−x et
MH=MB2=8−x2MH= \dfrac{MB}{2}=\dfrac{8-x}{2}MH=2MB=28−x
D'ou
KH2=....KH^2= ....KH2=....
-
NNadia-matheuse dernière édition par
J'ai trouvé pour KH² = 40 - 5x² / 4
Est-ce correcte ? J'ai fais 8 - x² + (8 - x/2²)
-
C'est KH2=(8−x)2−(8−x2)2=3(8−x)24KH^2=(8-x)^2-(\dfrac{8-x}{2})^2= \dfrac{3(8-x)^2}{4}KH2=(8−x)2−(28−x)2=43(8−x)2
- Ecris puis résous ensuite l'équation CM2=KH2CM^2=KH^2CM2=KH2
- Utilise la trigonométrie dans le triangle AMCAMCAMC.
-
NNadia-matheuse dernière édition par
Pouviez-vous me montrez le calcul à faire pour KH au carré s'il vous plaît? Je n'ai pas trouvé le même résultat.. J'ai trouvé 3x² - 48x + 149 / 4.
-
KH2=(8−x)2−(8−x2)2KH^2=(8-x)^2-(\dfrac{8-x}{2})^2KH2=(8−x)2−(28−x)2
Tu factorises (8−x)2(8-x)^2(8−x)2
KH2=(8−x)2(1−14)KH^2= (8-x)^2(1-\dfrac{1}{4})KH2=(8−x)2(1−41)
soit :
KH2=(8−x)2×34=3(8−x)24KH^2=(8-x)^2\times \dfrac{3}{4}= \dfrac{3(8-x)^2}{4}KH2=(8−x)2×43=43(8−x)2Si tu développes le carré
KH2=(x2−16x+64)×34=3x2−48x+1924KH^2= (x^2-16x+64)\times \dfrac{3}{4} = \dfrac{3x^2-48x+192}{4}KH2=(x2−16x+64)×43=43x2−48x+192
-
NNadia-matheuse dernière édition par
D'accord merci, du coup pour le résultat de l'équation 16 + x² = 3(8 - x²)/ 4 j'ai trouvé
x² + 48x - 128 = 0 qui a deux solution x1 : -40 - 16√11 /2 = -50,533 et x2 : -48 + 16√11 /2 = 2,53 donc je suppose qu'ici la valeur de CM²= KH² est 2,53² (environ 6,04), pour le 4e je ne sais pas comment faire car nous n'avons pas encore vu la trigonométrie en classe
-
Attention à l'écriture c'est (8−x)2(8-x)^2(8−x)2
La réponse est bien x2x_2x2.Pour la dernière question :
AM=AC×tan30°AM= AC\times tan30°AM=AC×tan30° ou vu que tu as un angle de 60°, tu considères la moitié d'un triangle équilatéral, soit à résoudre : x2+42=(2x)2x^2+4^2= (2x)^2x2+42=(2x)2
-
NNadia-matheuse dernière édition par
J'ai fais ce calcul et j'ai trouvé 2,30... on peut en conclure que les points ne sont pas alignés ?
-
Oui, les points ne sont pas alignés si CM=KHCM= KHCM=KH.
-
NNadia-matheuse dernière édition par
D'accord c'est noté ! Merci beaucoup pour votre aide.

Passez une bonne fin de journée !