Inéquation 1ère spécialité

Bonjour, pourriez-vous m’aider s’il vous plaît merci d’avance.
Une entreprise fabrique des appareils photographiques.
Pour x appartenant à l'intervalle [10; 60], on donne le bénéfice égal à
B(x) = -0,2x² + 12x - 50 en dizaine d'euros réalisé par la vente de x appareils.

a) Résoudre l'inéquation B(x) ≥ 0.
b) Interpréter le résultat obtenu.
a) Construire alors le tableau de variation de la fonction B sur [10; 60].
b) Déterminer alors la quantité d'appareil à vendre pour obtenir un bénéfice
maximal ainsi que la valeur de ce bénéfice.
Calculer B'(x) la dérivée de B.

@islarls Bonjour,

Indique tes éléments de réponse et la question qui te pose problème.

a) Factorise $B (x)$ et fais un tableau de signes.

Pour la première question j’ai utilisé delta et j’ai trouvé delta=104 mais je suis bloqué au tableau de variation

Bonsoir,

@islarls , tu peux continuer sur cette voie si tu le souhaites , pour résoudre $B(x)≥0B(x)\ge 0$

Vu que $Δ>0\Delta \gt 0$ , tu cherches les solutions $x_1$ et $x_2$ de $B (x) = 0$
Ensuite, tu détermines de signe de $B (x)$ polynôme du second degré (signe de $a$ , signe de $- a$ , signe de $a$ ) , avec $a = - 0.2$

Regarde le paragraphe II ici , si besoin :
https://www.mathforu.com/premiere-s/le-second-degre-2eme-partie/

@islarls

Pour le tableau de variations, utilise le cours sur la parabole.

@Noemi d’accord merci beaucoup mais je n’ai toujours pas compris comment former le tableau

@islarls

Tu es bloqué au tableau de variations ou au tableau de signes ?
Regarde ces cours :
https://www.mathforu.com/seconde/factorisation-et-etude-de-signes-en-2nd/
https://www.mathforu.com/premiere-s/le-second-degre-1ere-partie/
https://www.mathforu.com/premiere-s/le-second-degre-2eme-partie/

@Noemi @mtschoon
Bonjour, j’ai retravaillé mon cours et j’ai réussi à m’en sortir merci de votre réponse et de votre aide.

@islarls
A)
a) To solve the inequality B(x) ≥ 0, we need to find the values of x for which the function B is greater than or equal to 0.

To do this, we can start by setting B(x) equal to 0 and solving for x:

-0.2x^2 + 12x - 50 = 0

This is a quadratic equation, and we can solve it using the quadratic formula:

x = (-12 +/- sqrt(144 + 2000)) / (-0.4)

x = (-12 +/- sqrt(2144)) / (-0.4)

x = (-12 +/- 46.4) / (-0.4)

x = (-58.4, -5.6)

Now that we have the roots of the quadratic equation, we can use them to find the intervals where B(x) is greater than or equal to 0.

Since B(x) is a quadratic function, it will have a parabolic shape, with a single minimum or maximum value. If the parabola is facing upwards (like a "smile"), then the function will have a minimum value. If the parabola is facing downwards (like a "frown"), then the function will have a maximum value.

In this case, the parabola is facing downwards, so B(x) will have a maximum value at the x-coordinate of the vertex of the parabola. The x-coordinate of the vertex is given by the formula x = -b / (2a), where a and b are the coefficients of the x^2 and x terms, respectively.

Plugging in the values for a and b, we get:

x = -12 / (-0.4)

x = 30

At x = 30, B(x) has a maximum value. To find the y-coordinate of the vertex, we can plug x = 30 back into the original equation for B(x):

B(30) = -0.230^2 + 1230 - 50

B(30) = -180 + 360 - 50

B(30) = 130

So, the maximum value of B(x) is 130.

Since the parabola is facing downwards, B(x) will be less than or equal to 0 for all x-values less than the x-coordinate of the vertex (that is, for x < 30), and B(x) will be greater than or equal to 0 for all x-values greater than the x-coordinate of the vertex (that is, for x > 30).

Therefore, the solution to the inequality B(x) ≥ 0 is x ∈ (30, ∞).

@islarls

b) The result we obtained means that the function B(x) is greater than or equal to 0 for all x-values greater than 30. This means that if the company sells more than 30 devices, it will make a profit (that is, its revenue will be greater than its costs).

@islarls
2a)
To construct the table of variation for the function B(x) on the interval [10, 60], we can start by evaluating B(x) at a few points within that interval and seeing how the function behaves.

For example, we can evaluate B(x) at x = 10, 20, 30, 40, 50, and 60:

x B(x)
10 -50
20 10
30 130
40 230
50 310

@islarls
3)
To find the derivative of the function B(x), we can use the power rule for derivatives:

If f(x) = x^n, then f'(x) = n*x^(n-1)

Using the power rule, we can find the derivative of B(x) as follows:

B'(x) = (-0.22)x^(-0.22-1) + 12x^(12-1)

B'(x) = (-0.4)x^(-2) + 12x^(11)

B'(x) = -0.2x^(-2) + 12x^(11)

B'(x) = -0.2 / x^2 + 12*x^(11)

So, the derivative of the function B(x) is B'(x) = -0.2 / x^2 + 12*x^(11).

Bonjour,

@islarls a dit dans Inéquation 1ère spécialité :

Une entreprise fabrique des appareils photographiques.
Pour x appartenant à l'intervalle [10; 60], on donne le bénéfice égal à
B(x) = -0,2x² + 12x - 50 en dizaine d'euros réalisé par la vente de x appareils.

a) Résoudre l'inéquation B(x) ≥ 0.
b) Interpréter le résultat obtenu.

a) Construire alors le tableau de variation de la fonction B sur [10; 60].
b) Déterminer alors la quantité d'appareil à vendre pour obtenir un bénéfice
maximal ainsi que la valeur de ce bénéfice.

Calculer B'(x) la dérivée de B.

@islarls , pour que tu puisses vérifier tes résultats si besoin, je te mets quelques indications.

Pour le 1), le calcul de $x_1$ et $x_2$ solutions de $B (x) = 0$ tu as dû trouver après simplifications :
$x1=5−626x_1=5-6\sqrt{26}$ d'où $x1≈4.5x_1\approx 4.5$
$x2=5+626x_2=5+6\sqrt{26}$ d'où $x2≈55,5x_2\approx 55,5$

En utilisant le signe d'un polynôme du second degré, tu obtiens le signe de $B (x)$ sur $R$ :

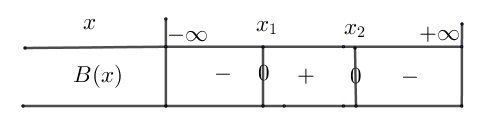
En restreignant à l'intervalle [10,60], tu obtiens :

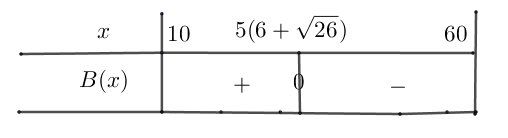
En travaillant sur cet intervalle [10,60], on peut déduire que le bénéfice est positif lorsque l'on vend entre 10 et 55 appareils.

@islarls ,

Pour le sens de variation de la fonction $B$ , tu peux utiliser le cours sur le sens de variation d'un polynôme du second degré $ax^2+bx+c$
Pour $\lt 0$ le maximum est pour $x=−b2a=30x=-\dfrac{b}{2a}=30$ .
$f (30) = 110$

Tu aurais pu aussi calculer la dérivée et son signe ( dérivée demandée en 3).
Pour qu'elle serve, je l'indique ici : $B^{'} (x) = - 0.4 x + 12$

Je mets le tout dans le tableau de variation de $B$ sur $[10, 60]$

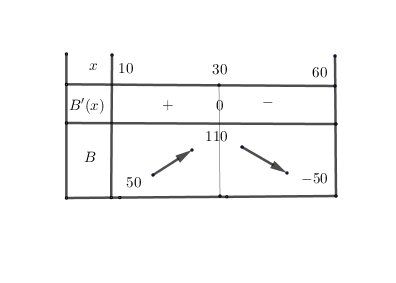
Tout peut se retrouver dans la représentation graphique de la fonction $B$ (graphique non demandé dans l'exercice)
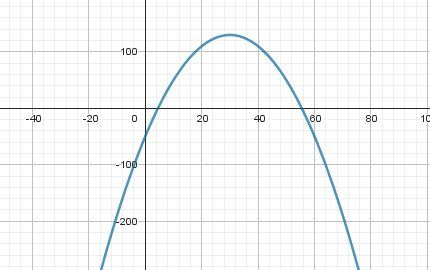
paraboleBénéfice.jpg

Bonne vérification éventuelle.