Pour chacune des fonctions suivantes, donner l'expression de sa dérivée f’ :
-
Ss 1 dernière édition par
Pour chacune des fonctions suivantes, donner l'expression de sa
dérivée f’ :- f(x)= x^4 -2x-3
2)f(x)= x^2-5x
3)f(x)= (x^2-1)√x - f(x) = 1 - 3x + √x
- f(x) = (3x + 2)/(x ^ 2 + 1)
- f(x)= x^4 -2x-3
-
@s-1 Bonjour, (Marque de politesse à ne pas oublier !!)
Indique tes éléments de réponse et la ou les dérivées qui te posent problème.
f(x)=x4−2x−3f(x) = x^4-2x-3f(x)=x4−2x−3 ; f′(x)=4x3−2f'(x)= 4x^3-2f′(x)=4x3−2
....
-
Ss 1 dernière édition par
@Noemi oui dsl enfainte je n'ai pas reussis a faire l'exercice
-
Applique le cours.
La dérivée de ax+bax+bax+b est aaa
La dérivée de xnx^nxn est nxn−1nx^{n-1}nxn−1
La dérivée de x\sqrt xx est 12x\dfrac{1}{2\sqrt x}2x1
....indique tes calculs.
-
Ss 1 dernière édition par
@Noemi 1)4x3−2
2)2x−5
-
Ss 1 dernière édition par
@s-1 3)
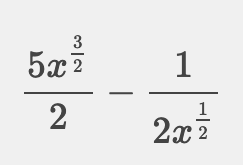
-
Oui pour la dérivée 2.
Pour la dérivée 3, le résultat indiqué est juste. il doit être justifié.c'est un produit u(x)×v(x)u(x) \times v(x)u(x)×v(x)
f(x)=(x2−1)xf(x)= (x^2-1)\sqrt xf(x)=(x2−1)x
tu poses u(x)=x2−1u(x) = x^2-1u(x)=x2−1, tu calcules u′(x)u'(x)u′(x)
tu poses v(x)=xv(x)= \sqrt xv(x)=x,
La dérivée de u(x)×v(x)u(x)\times v(x)u(x)×v(x) est u′(x)×v(x)+u(x)×v′(x)u'(x)\times v(x)+u(x)\times v'(x)u′(x)×v(x)+u(x)×v′(x)Je te laisse indiquer tes calculs.
-
Ss 1 dernière édition par
@Noemi 4)
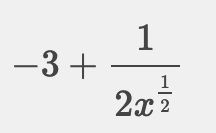
-
Ss 1 dernière édition par
@Noemi 5)
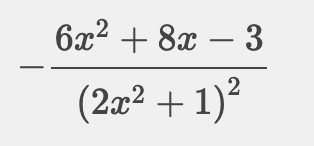
-
La 5 est fausse ou une erreur dans l'énoncé du dénominateur de la fonction.
(Le 2 devant le xxx ? )
-
Ss 1 dernière édition par
@Noemi oui c devant
-
L'expression de la fonction 5 serait donc : f(x)=3x+22x2+1f(x)=\dfrac{3x+2}{2x^2+1}f(x)=2x2+13x+2 ?
-
Ss 1 dernière édition par
@Noemi non 3x+2/ x^2+1
-
Donc ta réponse est fausse.
-
Ss 1 dernière édition par
@Noemi 5)
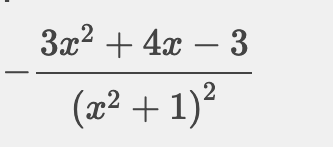
-
Ss 1 dernière édition par
@Noemi Est-ce que vous pouvez m'aider a reformuler mes reponses svp?
-
Je t'ai indiqué la méthode à utiliser, suis la et indique tes calculs si tu souhaites une vérification.
Ecrire ou recopier le résultat (fourni par un site ? ) sans justification n'est pas une démonstration.