point proches Points éloigné dans la courbe
-
cake dernière édition par
bonsoir
comment déterminer les points les plus proches et les plus éloignés de l'origine de la courbe de l'équation x⁶+y ⁶ = 1
-
@Meriem-Mimi Bonjour,
Le multipost est interdit sur ce forum. Ton second post va être supprimé.
En quelle classe es-tu ?
-
BBlack-Jack dernière édition par
Bonjour,
On peut réduire l'étude pour x dans [0 ; 1] et y aussi.
On trouvera ainsi un point de distance max et un autre de distance min.Il y aura évidement 3 autres paires de points en inversant les signes de x et de y des coordonnées des points trouvés.
x^6 + y^6 = 1
y = (1-x^6)^(1/6) avec x dans [0 ; 1]Donc, un point P de la courbe représentant f(x) = (1-x^6)^(1/6) a pour coordonnées P(X ; (1-x^6)^(1/6)) (avec X dans 0;1)
On a donc OP² = X² + (1-X^6)^(1/3))
OP sera max pour la même valeur de X qui rends OP² maximal
OP sera min pour la même valeur de X qui rends OP² minimalIl faut donc étudier la fonction g(x) = X² + (1-X^6)^(1/3)) sur [0;1] et en trouver le max et le min
On étudie le signe de g'(x) = ...
Et on en déduit les coordonnées des points de distances min et max ...Voila, il n'y a plus qu'à ...
-
mtschoon dernière édition par mtschoon

Bonjour,
@Meriem-Mimi , si tu veux savoir les résultats à trouver, regarde :
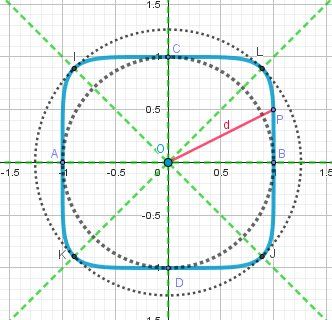
La distance d=OPd=OPd=OP est minimale pour PPP en AAA ou BBB ou CCC ou DDD
La distance d=OPd=OPd=OP est maximale pour PPP en III ou JJJ ou KKK ou LLLBons calculs !
-
cake dernière édition par
@mtschoon merci ,mais j'arrive pas à trouver conditions sur x et y
-
mtschoon dernière édition par mtschoon

@cake , bonjour,
La somme de 2 carrés x2x^2x2 et y2y^2y2 (donc positifs) est égale à 1, d'où conditions :
0≤x2≤10\le x^2\le 10≤x2≤1 et 0≤y2≤10\le y^2\le 10≤y2≤1
c'est à dire
−1≤x≤1-1\le x\le 1−1≤x≤1 et −1≤y≤1-1\le y\le 1−1≤y≤1