Le triangle impossible à construire

Bonjour.
Mon fils en 5eme a une énigme à résoudre et il bloque.

Construire en triangle avec
AB = 7 cm
L'angle ABC = 40°
BC +CA = 16 cm
Sans aucun calcul juste avec compas et rapporteur et règle

Si vous pouvez l'aider ?
Merci par avance.
Emeline

@Emeline38 Bonsoir,

Tracer le segment $\ cm$ .
A l'aide du rapporteur, marqué l'angle de 40° qui donne la demi droite $[B x)$ .
A partir du point $B$ tracé un cercle de centre $B$ et de rayon proche de 10 cm et à partir du point $A$ un cercle de rayon 6 cm. Il faut affiner la mesure des rayons des cercles pour que le point d'intersection des deux cercles appartiennent à la demi droite $[B x)$ .
La mesure de $B C$ doit être proche de 9,74 cm et celle de $A C$ , proche de 6,26 cm.

Merci beaucoup.
Il va essayer cet après-midi.

Emeline.

@Emeline38

Il essaie en traçant des cercles de rayon la précision de sa règle, soit 9,7 ; 9,8 cm à partir du point $B$ et de 6,2 : 6,3 cm à partir du point $A$ .

@Noemi

C'est tout bon !
Merci.

@Emeline38

C'est parfait.

Méthode plus rapide :
Tracer le segment $\ cm$ .
A l'aide du rapporteur, marquer l'angle de 40° qui donne la demi droite $[B x)$ .
Sur cette demi-droite, placer un point $D$ tel que $\ cm$ .
Tracer à l'aide du compas la médiatrice du segment $[A D]$ , elle coupe le segment $[B D]$ en $C$ .

@Noemi a dit dans Le triangle impossible à construire :

@Emeline38

C'est parfait.

Bonjour,

Alternative

a) On trace AB = 7 cm (rouge sur mon dessin)
b) On trace la direction de (BC) en utilisant le rapporteur.
c) On trace un arc de cercle de centre B et de rayon 16 cm qui coupe le (BC) en D (ou on mesure à la règle) (en bleu sur mon dessin)
d) On place la pointe sèche du compas quelque part sur le segment [B;D] et on trace le cercle passant par D, si il passe par le point A, le point C est où était la pointe sèche du compas.
sinon ...
On revient au point (d) en déplaçant la pointe sèche du compas sur [BD]
... et on recommence le proche en proche jusqu'à ce que le cercle passe par A.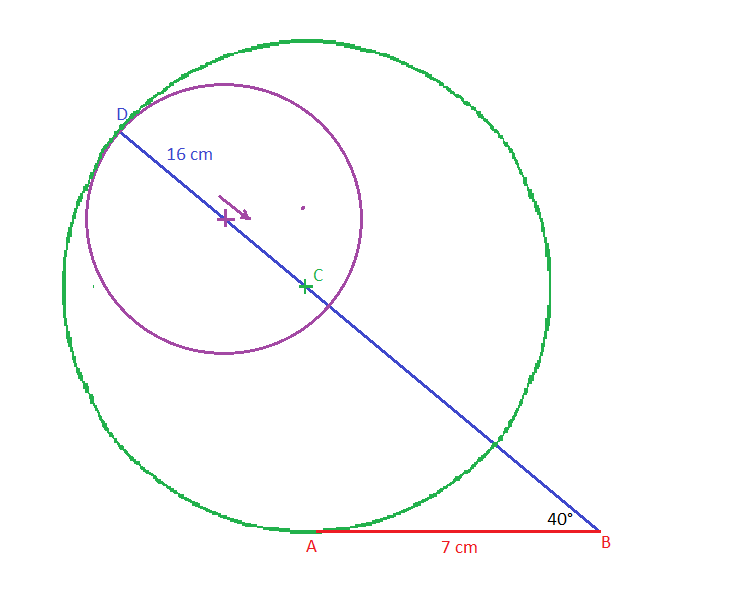

Sans titre.png

@Noemi

Effectivement cette méthode est sûrement la solution car le prof a rajouté qu'il fallait connaître les mediatrices!
Merci beaucoup

Ce message a été supprimé !