Limites de fonctions
-
Lucas_rst dernière édition par

Bonjour je doit trouver les limites en + et - l’infini point la fonction g(x)=(x+2)e**x-4 -2
Mais je ne sais pas comment faire est ce que quelqu’un pourrait m’aider svp ?
-
@Lucas_rst Bonjour,
L'expression de la fonction ggg est t-elle : g(x)=(x+2)ex−4−2g(x) = (x+2)e^{x-4}-2g(x)=(x+2)ex−4−2 ?
Utilise les limites de référence du cours.
-
Lucas_rst dernière édition par

Ce message a été supprimé !
-
Lucas_rst dernière édition par

@Noemi oui et c’est juste en - l’infini que je n’arrive pas à trouver la limite
-
Quelle est la limite de xexxe^xxex quand xxx tend vers −∞-\infty−∞ ?
-
Lucas_rst dernière édition par

@Noemi c’est bon j’ai trouver cela fait -2 merci quand même pour votre aide
-
Exact, -2.
-
mtschoon dernière édition par mtschoon

Bonjour,
@Lucas_rst , j'espère que tu as prouvé les limites en +∞+\infty+∞ et −∞-\infty−∞ correctement.
Si j'ai bien lu : g(x)=(x+2)ex−4−2g(x)=(x+2)e^{x-4}-2g(x)=(x+2)ex−4−2
En +∞+\infty+∞, il n'y a pas d'indétermination.
limx→+∞g(x)=+∞\displaystyle \lim_{x\to +\infty} g(x)=+\inftyx→+∞limg(x)=+∞En −∞-\infty−∞, il y a une indétermination à lever
Pour utiliser une propriété usuelle, il faut transformer g(x)g(x)g(x)
g(x)=(x+2)ex+2−6−2g(x)=(x+2)e^{x+2-6}-2g(x)=(x+2)ex+2−6−2
g(x)=(x+2)ex+2−6−2g(x)=(x+2)e^{x+2-6}-2g(x)=(x+2)ex+2−6−2
g(x)=(x+2)ex+2e−6−2g(x)=(x+2)e^{x+2}e^{-6}-2g(x)=(x+2)ex+2e−6−2En posant X=x+2X=x+2X=x+2, vu que limX→−∞XeX=0\displaystyle \lim_{X\to -\infty}Xe^X=0X→−∞limXeX=0 , tu déduis que : limx→−∞(x+2)ex+2=0\displaystyle \lim_{x\to -\infty}(x+2)e^{x+2}=0x→−∞lim(x+2)ex+2=0
Donc :
limx→−∞g(x)=0×e−6−2=0−2=−2\displaystyle \lim_{x\to -\infty}g(x)=0\times e^{-6}-2=0-2=-2x→−∞limg(x)=0×e−6−2=0−2=−2
-
mtschoon dernière édition par mtschoon

Illustration graphique :
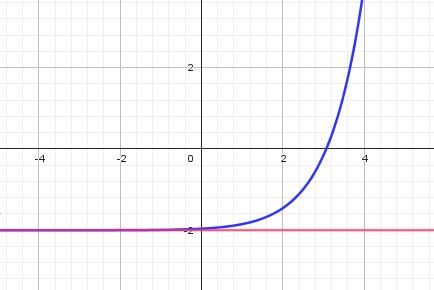
La représentation graphique de ggg est en bleu
L'asymptote horizontale en −∞-\infty−∞, d'équation y=−2y=-2y=−2, est en rouge.Vu l'expression de la fonction, la courbe est "très proche" de l'asymptote.