projete orthogonal et calcul d angles

bonjour quelq un pourrait m aider s il vous plait
M, N, I sont trois points de l'espace. I' est le pro- jeté orthogonal de I sur la droite (MN) et l' se trouve entre les

points M et N. On donne : MN=5, MI = 4 et MI' = 2.

a) Calculer MN-MI.

b) En déduire la mesure, en degré, de l'angle IMN.
c) Calculer la longueur NI. Arrondir au dixième.
j ai essayer de le faire mais je pense avoir faux pour le premier j ai juste fait 5 fois 4 et j ai trouvé 20 et le deuxieme je connais la formule mais je sais pas comment faire
merci d avance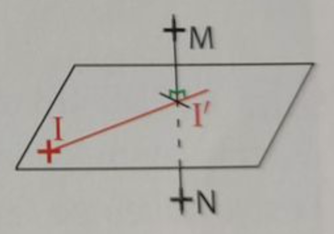

Scan mis en forme par la modération du site.

@fariss Bonjour,

Indique tes calculs.
Tu écris la relation et tu complètes les termes connus par leur valeur.

pour le petit a mn=5 et mi=4 donc mn fois mi=5 fois 4=20
pour le petit b puice que I' est le projeté orthogonal de I et I'=1/2 MN alors IMN est un triangle
équilateral donc l angle IMN=60 degrés ,pour le petit c j ai pas d idée

Bonjour,

@fariss ,
Revois tes explications du a) et du b)

Théorème de la projection
$MN→.MI→=MN×MI′=5×2=10\overrightarrow{MN}.\overrightarrow{MI}=MN\times MI'=5\times 2=10$

Pour le b), utilise la définition usuelle du produit scalaire
$MN→.MI→=MN×MI×cos⁡IMN^\overrightarrow{MN}.\overrightarrow{MI}=MN\times MI\times \cos{\widehat{IMN}}$

Tu remplaces les 3 quantités connues par leurs valeurs et tu déduis $cos⁡IMN^\cos{\widehat{IMN}}$ puis $IMN^\widehat{IMN}$ qui vaut bien $60$ °

@fariss ,

Pour le c), tu peux calculer $I I^{'}$ en prenant le sinus de $IMI′^\widehat{IMI'}$ dans le triangle $I M I^{'}$
Connaissant $I I^{'}$ et $I^{'} N$ , avec le théorème de Pythagore dans le triangle rectangle $I I^{'} N$ , tu obtiendras $NI^2$ puis $N I$

ok merci

De rien @fariss .
Tu peux donner tes réponses au c) si tu souhaites une vérification.

Bonsoir j ai trouvé que le sinus de IMI'=30 degrés mais je comprend pas comment je peux trouver II'

@fariss Bonsoir,

$IMN^=IMI′^=60\widehat{IMN}= \widehat{IMI'} = 60$ °

Quelle est l'expression de $sin(IMI′^)sin(\widehat{IMI'})$ ?

Moi j avais fais sin IMI'=2/4=0.5 ASIN(0.5)=30

@fariss , tu fais des confusions

Dans le triangle rectangle $I M I^{'}$ :

$sinIMI′^=II′IMsin\widehat{IMI'}=\dfrac{II'}{IM}$ (côté opposé/hypothénuse)

et tu sais que $sinIMI′^=sin60sin\widehat{IMI'}=sin60$ °= $32\dfrac{\sqrt 3}{2}$

Tu dois pouvoir trouver $I I^{'}$

@fariss , bonjour,

Pour que tu puisses vérifier, je t'indique des résultats.

Sauf erreur, $II′=23II'=2\sqrt 3$ puis $NI=21NI=\sqrt{21}$

bonjour j ai bel et bien trouver que II'=2racine de 3 mais je me demandais comment je peux trouver IN si je connais qu une valeur dans le triangle rectangle

@fariss

Avec les données de l'énoncé, tu peux calculer la distance $I^{'} N$ .

ah ok c est bon merci

@mtschoon j ai trouvé ces 2 donnés merci beacoup de votre aide

@fariss

Parfait si tu as pu terminer l'exercice et trouver le résultat indiqué.

@fariss a dit dans projete orthogonal et calcul d angles :

@mtschoon j ai trouvé ces 2 donnés merci beacoup de votre aide.

C'est très bien @fariss .