L'éclair dans le carré

Bonjour,

Avez-vous un début de piste pour moi?
Merci d'avance.

Scan supprimé par la modération du forum.

Le scan ou un lien de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques ou figures sont autorisés.
Écris l'énoncé, tes éléments de réponse et indique la question qui te pose problème. Tu obtiendras alors des pistes de résolution.

Le scan va être supprimé par la modération du site.

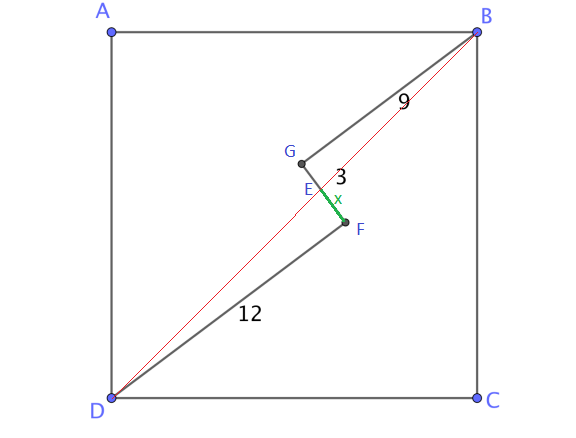
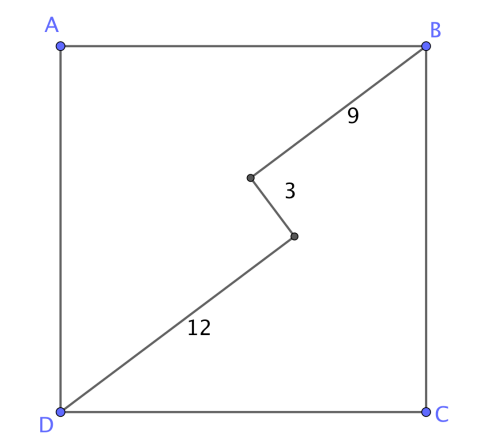
On considère un carré. A partir d'un sommet on trace un segment de longueur 12. Puis on trace le segment de longueur 3 perpendiculaire au précédent comme indiqué sur la figure ci-dessous. Enfin on trace le segment perpendiculaire au précédent, de longueur 9, qui a pour extrémité le sommet opposé du carré.
Déterminer la longueur du côté du carré.

Voilà mes pistes:
soit a le côté du carré, d la diagonale [BD]
a= (d√2) : 2

Merci pour votre aide.

@RémiKADO Bonjour,

Très bien, tu as suivi les consignes.
Trace la diagonale $[B D]$ , puis utilise la propriété de Thalés (en justifiant le parallélisme) et les relations sur les rapports égaux.

Bonjour,

En se servant du fait que "Les triangles DFE et BGE sont semblables" ou bien par Thales, on a :

x/12 = (3-x)/9
9x = 36 - 12x
21x = 36
x = 12/7

On connait DF = 12 et EF = x = 12/7 --> On peut calculer DE (par Pythagore)
On connait GB = 9 et GE = 3-x = 3 - 12/7 --> On peut calculer BE (par Pythagore ou Thales)

On en déduit la longueur de BD (par BD = DE + BE)

Et on calcule un coté du carré par BE/(RacineCarrée(2)... on trouve : coté = 15

Il n'y a plus qu'à ...

Ou bien appliquer une autre méthode (il y en a plusieurs)

Sans titre.png