Géométrie du secteur sphérique
-
GGuy dernière édition par
Bonjour,
Je me nomme Guy et je suis un prof de math-science au secondaire et je m'adresse à cette communauté pour essayer d'obtenir une réponse à un problème de géométrie sur les secteurs sphériques définis par la proximité de deux sphères. Le schéma fourni ci-bas expose le problème en soi. Je cherche une équation qui me permettrait de trouver à coup sûr l'angle au sommet de chacun des deux secteurs sphériques suivants. Les paramètres en cause sont: - la dimension de chacune des sphères et la distance qui les sépare. Je veux être en mesure de connaître (à volonté) quel sera l'angle des secteurs respectifs si la distance entre les deux sphères varie et ce, afin de calculer le volume de chacun des secteurs sphériques impliqués! Il est plutôt facile de trouver la formule pour calculer le volume d'un secteur sphérique quand on connaît déjà l'angle au sommet. Le problème survient quand on se rend compte que les droites définissant les limites extérieures de l'angle au sommet sont des points tangents qui se modifient si on éloigne ou rapproche le corps B ou le corps A. Merci de votre aide.
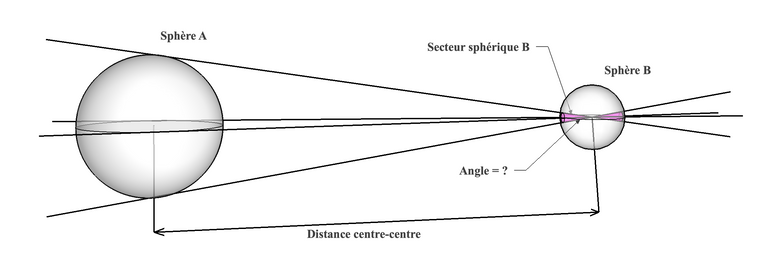
-
BBlack-Jack dernière édition par
Bonjour,
Je ne suis pas sûr d'avoir bien interprété ta demande.
Il me semble que ta demande se résume à calculer la valeur de l'angle au sommet du secteur sphérique B par exemple.
Sur mon dessin : OP est perpendiculaire à O'P et donc :OP = OO'.sin(OO'P)
R = D.sin(OO'P)
angle(OO'P) = arcsin(R/D)Angle(PO'Q) = 2 * arcsin(R/D), c'est la mesure de l'angle au sommet du secteur sphérique B.
Ce qui devrait donner : Volume du secteur sphérique D = 2/3 * Pi * r² * h avec h = r * (1 - cos(OO'P))
Vol(sec B) = 2/3 * Pi * r² * r * (1 - cos(OO'P))
Vol(sec B) = 2/3 * Pi * r³ * r * (1 - cos(arcsin(R/D))
Vol(secB)=23∗π∗r3∗(1−1−(RD)2)Vol_{(sec B)} = \frac{2}{3} * \pi * r^3 * (1 - \sqrt{1 - (\frac{R}{D})^2})Vol(secB)=32∗π∗r3∗(1−1−(DR)2) avec D > R
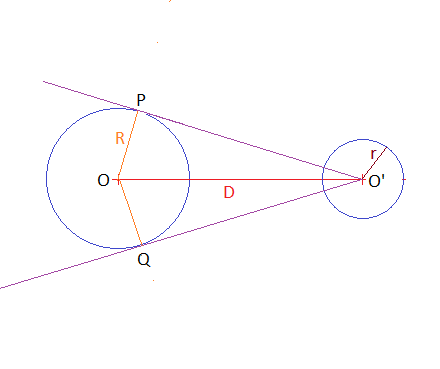
Aucun calcul vérifié et je ne suis pas matheux ... donc prudence.
-
GGuy dernière édition par
@Black-Jack
Merci beaucoup pour cette belle démonstration et le schéma explicatif. Je suis un peu frustré de ne pas avoir constaté qu'en fait, il existait nécessairement un rayon perpendiculaire au point de tangence, et de facto, un triangle rectangle nous permettant de résoudre le tout par un rapport trigonométrique relativement simple! Tout me semble bien cohérent. Merci encore.