Fonction du troisième degré, extrémum, tangente
-
noamii dernière édition par Noemi
bonsoir besoin d'aide svp pour cette partie d'un exercice dérivabilité concernant les extrema
et merci bcq
ex:
on considère la fonction f définie par f(x)=x³+ax²+bx+3 où a et b deux rééls.
on désigne (c) sa courbe représentative dans un repère orthonormé R(o,i,j).- déterminer les rééls a et b sachant que f admet un extremum local en 2 égal à -1.
- a)dresser le tableau de variation de la fonction f et préciser les extrema locaux de f.
b)écrire une équation cartésienne à la tangente T à la courbe c au pt I d'abscisse 1
c) étudier la position relative de T et (C)
3)déterminer les points de (C) où la tangente est parallèle à la droite T':y-9x+1=0
-
mtschoon dernière édition par mtschoon

@noamii , bonsoir,
f(x)=x3+ax2+bx+3f(x)=x^3+ax^2+bx+3f(x)=x3+ax2+bx+3 donc f′(x)=3x2+2ax+bf'(x)=3x^2+2ax+bf′(x)=3x2+2ax+b
f admet un extremum local en 2 égal à -1 se traduit par :
f(2)=−1f(2)=-1f(2)=−1
f′(2)=0f'(2)=0f′(2)=0Tu obtiendras ainsi un système de deux équations à 2 inconnues aaa et bbb à résoudre.
Bons calculs.
-
mtschoon dernière édition par

@noamii ,
Après calculs, sauf erreur, tu dois trouver a=−3a=-3a=−3 et b=0b=0b=0
d'où
f(x)=x3−3x2+3f(x)=x^3-3x^2+3f(x)=x3−3x2+3Reposte si besoin.
-
mtschoon dernière édition par mtschoon

@noamii ,
Schéma pour que tu puisses vérifier le sens de variation de (f), l'équation de (T) et la position de (T) par rapport à (C)
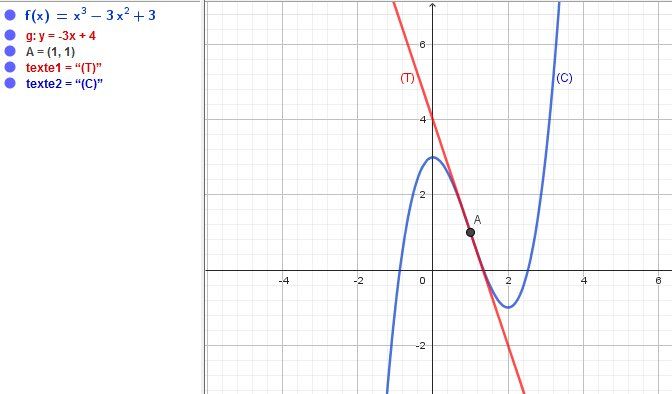
-
noamii dernière édition par
@mtschoon mrc bcq
-
noamii dernière édition par
@mtschoon mrc bcq juste je voulais savoir si vous pouvez svp me donner une idée sur la résolution de la 3eme question détermination d'un pt où la tangente est parallèle à une droite
-
mtschoon dernière édition par mtschoon

@noamii ,
Deux droites sont parallèles ssi elles ont même coefficient directeur
y−9x+1=0y-9x+1=0y−9x+1=0 <=> y=9x−1y=9x-1y=9x−1 coefficient directeur 999La tangente en un point d'abscisse x0x_0x0 de la courbe a pour coefficient directeur f′(x0)f'(x_0)f′(x0)
Tu dois donc trouver les valeurs x0x_0x0 telles que f′(x0)=9f'(x_0)=9f′(x0)=9
En bref, tu dois trouver les solutions de l'équation f′(x)=9f'(x)=9f′(x)=9 c'est à dire les solutions de 3x2−6x=93x^2-6x=93x2−6x=9
-
noamii dernière édition par
@mtschoon a ouiii c vrai mrc bien!
-
noamii dernière édition par
Ce message a été supprimé !
-
mtschoon dernière édition par

@noamii , de rien .
J'espère que tu as trouvé, pour ta dernière question, les points de coordonnées (−1,−1)(-1,-1)(−1,−1) et (3,3)(3,3)(3,3)
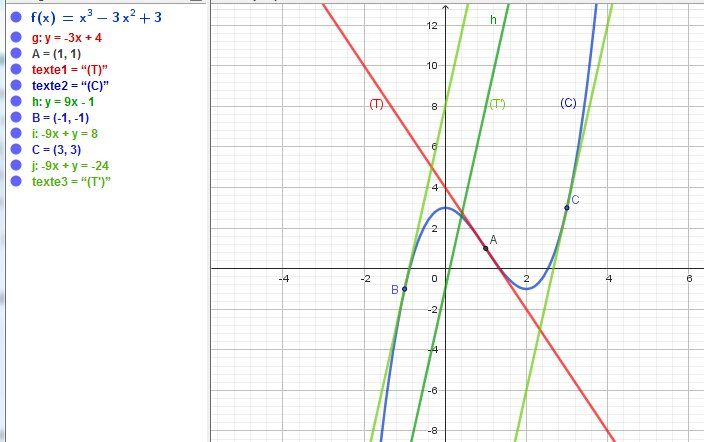
Bon travail.
-
noamii dernière édition par noamii
@mtschoon c bon je les ai trouvés mrc bcq
-
mtschoon dernière édition par

@noamii , parfait !
-
noamii dernière édition par noamii
@mtschoon concernant la position relative j'ai calculer f(x)-(-3x+4) et j'ai trouvé un polynôme 3eme degré dont le racine est 1 après je l'ai factorisé et fait le tableau de signe mais je trouve tjrs que la courbe est au dessus de la droite alors qu'elle est au dessous de C au voisinage de ]-l'infini,1] est ce que ma démarche est fausse?
-
@noamii Bonjour,
Quelle factorisation trouves-tu pour f(x)−(−3x+4)f(x)-(-3x+4)f(x)−(−3x+4) ?
-
noamii dernière édition par
@Noemi bonjour,
c'est (x-1)(x²-2x+1)
-
@noamii
Oui et
x2−2x+1=(x−1)2x^2-2x+1=(x-1)^2x2−2x+1=(x−1)2
donc l'expression est du signe de (x−1)(x-1)(x−1).
je te laisse conclure.
-
noamii dernière édition par
@Noemi positive +
-
x−1x-1x−1 est positif si x.....x .....x.....
x−1x-1x−1 est négatif si x.....x .....x.....
-
noamii dernière édition par
@Noemi x-1 est positive si x=1
x-1 est négatif si x=-1
et dans ce cas c'est + c'est ça?
-
Non,
x−1>0x-1\gt0x−1>0 si x>1x \gt1x>1
x−1<0x-1\lt 0x−1<0 si x<1x\lt1x<1
x−1=0x-1= 0x−1=0 si x=1x= 1x=1
-
noamii dernière édition par
@Noemi a oui ouii c vrai je me suis trompée c'est bon je trouve le bon résultat maintenant merci bien!
-
Parfait si tu as tout compris.
-
mtschoon dernière édition par mtschoon

@noamii ,
Eventuellement,
Une autre façon de procéder pour f(x)−(−3x+4)f(x)-(-3x+4)f(x)−(−3x+4)
f(x)−(−3x+4)=x3−3x2+3x−1f(x)-(-3x+4)=x^3-3x^2+3x-1f(x)−(−3x+4)=x3−3x2+3x−1
Si tu connais l'identité remarquable
(a−b)3=a3−3a2b+3ab2−a3(a-b)^3=a^3-3a^2b+3ab^2-a^3(a−b)3=a3−3a2b+3ab2−a3 ,
tu trouves directement :
f(x)−(−3x+4)=(x−1)3f(x)-(-3x+4)=(x-1)^3f(x)−(−3x+4)=(x−1)3(x−1)3(x-1)^3(x−1)3 est du signe de (x−1)(x-1)(x−1) , d'ou la position que tu as trouvée.
Bon travail !