Les vecteurs en seconde

Exercice :
Je bloque sur cet exercice j'ai besoin d'aide.
Soient les deux vecteurs A = ( 1 , α, β ) et B= ( 2 , -3 , 4 ).
Trouver α et β pour que le vecteur Α soit parallele à B puis déterminer le vecteur unitaire pour chacun des deux vecteurs.
J'ai besoin d'aide svp pour cet exercice.

@medou-coulibaly Bonjour, (Marque de politesse à ne pas oublier !)

Utilise le cours, :
Deux vecteurs sont colinéaires si ....

Bonjour,

@medou-coulibaly , comme te le dit @Noemi (modératrice), il ne faut pas oublier la formule de politesse (cela fait partie des consignes du forum).

On doit parler de vecteurs "colinéaires" (ce sont les droites-supports des vecteurs qui sont "parallèles").

Si tu as consulté ton cours, tu as dû voir qu'il faut chercher le réel $k$ tel que $A→=kB→\overrightarrow{A}=k\overrightarrow{B}$ , c'est à dire :
${1=2kα=−3kβ=4k\begin{cases}1=2k\cr \alpha =-3k\cr \beta=4k\end{cases}$

$1 = 2 k$ <=> $k=12k=\dfrac{1}{2}$

Tu remplaces $k$ par $12\dfrac{1}{2}$ dans les deux autres équations et tu trouveras $α\alpha$ et $β\beta$

Essaie de poursuivre.

@medou-coulibaly , bonjour,

J'espère que tu as trouvé les valeurs de $α\alpha$ et $β\beta$ :
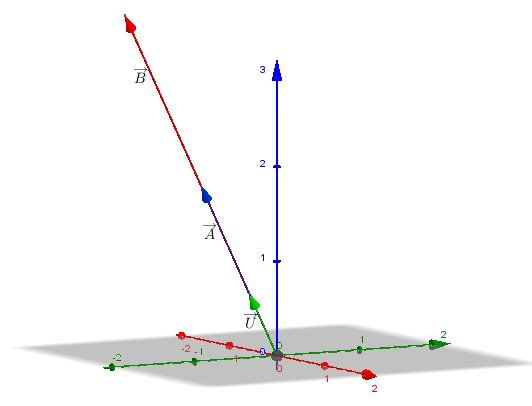
$α=−32\alpha=-\dfrac{3}{2}$ et $β=2\beta=2$

Dans un repère de l'espace, si l'on représente ces deux vecteurs à partir de l'origine du repère, ils sont portés par la même droite.
Un vecteur $U→\overrightarrow{U}$ unitaire colinéaire à l'un est forcément vecteur unitaire colinéaire à l'autre.

Par définition, un vecteur unitaire a pour norme 1

En utilisant $B→\overrightarrow{B}$ par exemple, le vecteur unitaire colinéaire à $B→\overrightarrow{B}$ et de même sens sera :
$U→=(1∣∣B→∣∣)×B→\overrightarrow{U}=\biggr(\dfrac{1}{||\overrightarrow{B}||}\biggr)\times \overrightarrow{B}$

Pour trouver les coordonnées de $U→\overrightarrow{U}$ , il te suffira de diviser les coordonnées de $B→\overrightarrow{B}$ par $∣∣B→∣∣||\overrightarrow{B}||$

Regarde ton cours pour calculer la norme d'un vecteur
Rappel :
Un vecteur $V→\overrightarrow{V}$ de coordonnées $(a, b, c)$ a pour norme :
$∣∣V→∣∣=a2+b2+c2||\overrightarrow{V}||=\sqrt{a^2+b^2+c^2}$

Remarque:
Si tu voulais le vecteur unitaire colinéaire à $B→\overrightarrow{B}$ et de sens contraire, ce sera :
$−(1∣∣B→∣∣)×B→-\biggr(\dfrac{1}{||\overrightarrow{B}||}\biggr)\times \overrightarrow{B}$

Bons calculs.

@mtschoon merci beaucoup madame je vais travailler dessus

Bon travail @medou-coulibaly .

@mtschoon ok merci beaucoup madame