3. Problème Loi binomiale

Problème Loi binomiale

  • D

    Bonjour j’ai un exo de math de terminale S sur les proba assez complexe, j’aimerai de l’aide.

    Un professeur pose 3 questions sous la forme d'un QCM.
    Pour chaque question, 4 réponses sont proposées dont une seule est correcte.
    Un élève décide de répondre au hasard.
    On note S l'événement : « la réponse à la question est exacte. »
    et E l'événement : « la réponse à la question est fausse. »
    On note X la variable aléatoire donnant le nombre total de bonnes réponses au questionnaire.

    1. Quelle loi suit X ? Préciser ses paramètres.
    2. Représenter la succession des trois résultats par un arbre pondéré.
    3. Calculer successivement la probabilité pour l'élève d'avoir 0, 1, 2, 3 bonnes réponses
      (valeurs exactes sous forme de fractions).
    4. Calculer E(X), l'espérance mathématique du nombre de bonnes réponses.
    5. Calculer V(X).
    N 1 réponse
  • N
    Modérateurs

    @dodo123 Bonjour,

    Indique tes éléments de réponse et la question qui te pose problème.

  • mtschoon

    Bonjour,

    @dodo123 , je t'indique quelques pistes pour démarrer,

    1 ) L'expérience est composée de 3 épreuves répétées indépendantes.
    A chaque épreuve :
    la probabilité d'un succès S (réponse exacte) est p=14p=\dfrac{1}{4}p=41​
    la probabilité d'un échec E (réponse fausse) est q=1−p=34q=1-p=\dfrac{3}{4}q=1−p=43​
    X représente le nombre de succès sur ces 3 épreuves.
    X suit donc la loi de Bernoulli B(3,14)B(3,\dfrac{1}{4})B(3,41​)

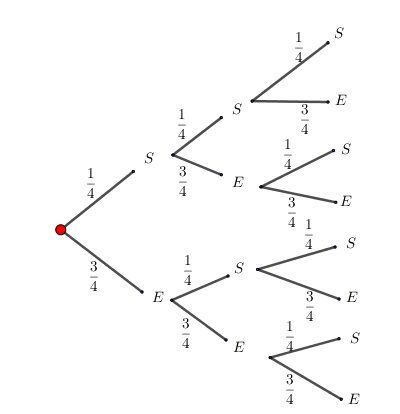
    2 ) Je te joins un arbre pondéréarbre3Niveaux.jpg

    Essaie de poursuivre et reposte si besoin.

  • mtschoon

    Bonjour @dodo123

    Lorsque tu auras compris les questions 1) et 2), pour 3) ,4) et 5) il te suffit d'utiliser ton cours.

    Pour la 3), tu peux faire les calculs avec l'arbre, vu qu'il est demandé.
    Eventuellement, tu peux utiliser la formule générale (ce qui reviendra au même)
    Pr(X=k)=(nk)pk(1−p)n−kPr(X=k)=\binom{n}{k}p^k(1-p)^{n-k}Pr(X=k)=(kn​)pk(1−p)n−k, avec n=3,p=14n=3,p=\dfrac{1}{4}n=3,p=41​ et k=k=k=(successivement) 0,1,2,30,1,2,30,1,2,3

    Pour la 4 ) et la 5), tu peux utiliser les définitions générales pour trouver E(x)E(x)E(x) et V(x)V(x)V(x)
    Pour une loi binomiale , si les formules sont dans ton cours, tu peux calculer plus rapidement avec :
    E(x)=npE(x)=npE(x)=np et V(x)=npq=np(1−p)V(x)=npq=np(1-p)V(x)=npq=np(1−p)

    Bons calculs.

Se connecter pour répondre