Conjecturer une position relative
-
HHex dernière édition par
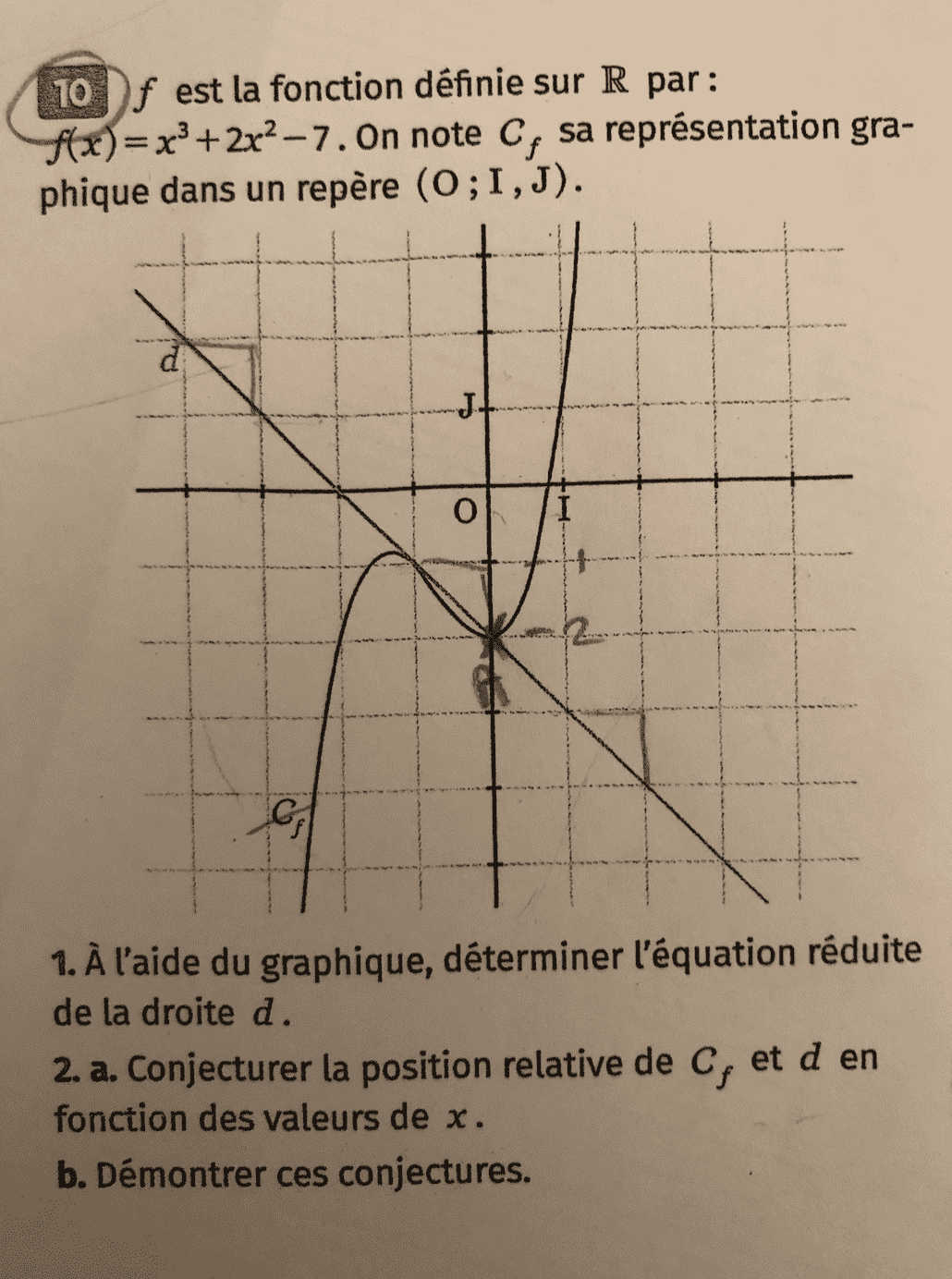
Bonjour sur cet exercice, il nous est dit : f est la fonction définie sur R par : f(x) = x^3+2x^2-7. On note Cf, sa représentation graphique dans un repère. (O, I, J).
- A l'aide du graphique, déterminer l'équation réduite de la droite d. J'ai trouvé grâce au graphique que l'équation de la droite était -x-2.
2.a. Conjecturer la position relative de Cf et d en fonction des valeurs de x. J'ai essayé de faire f(x)-d = 0 pour déterminer le point d'intersection mais il est impossible de factoriser x^3+2x^2-7-(-x-2). Je me suis donc demandé si on pouvait trouver le point d'intersection en disant qu'on l'avait trouvé à l'aide de la calculatrice et ensuite on disait que comme f(x) était au dessus ou en dessous de d f(x)-d était négatif ou positif.
Cependant la question b de la 2e question me demande de démontrer les conjectures. Je ne sais donc pas comment faire car j'ai trouvé le point d'intersection à l'aide de la calculatrice. Faut-il que je prouve ces conjectures en soustrayant des point de f(x) et de d pour prouver mes conjectures?
Vous trouverez l'exercice complet et une représentation graphique des courbes faite en ligne en PJ.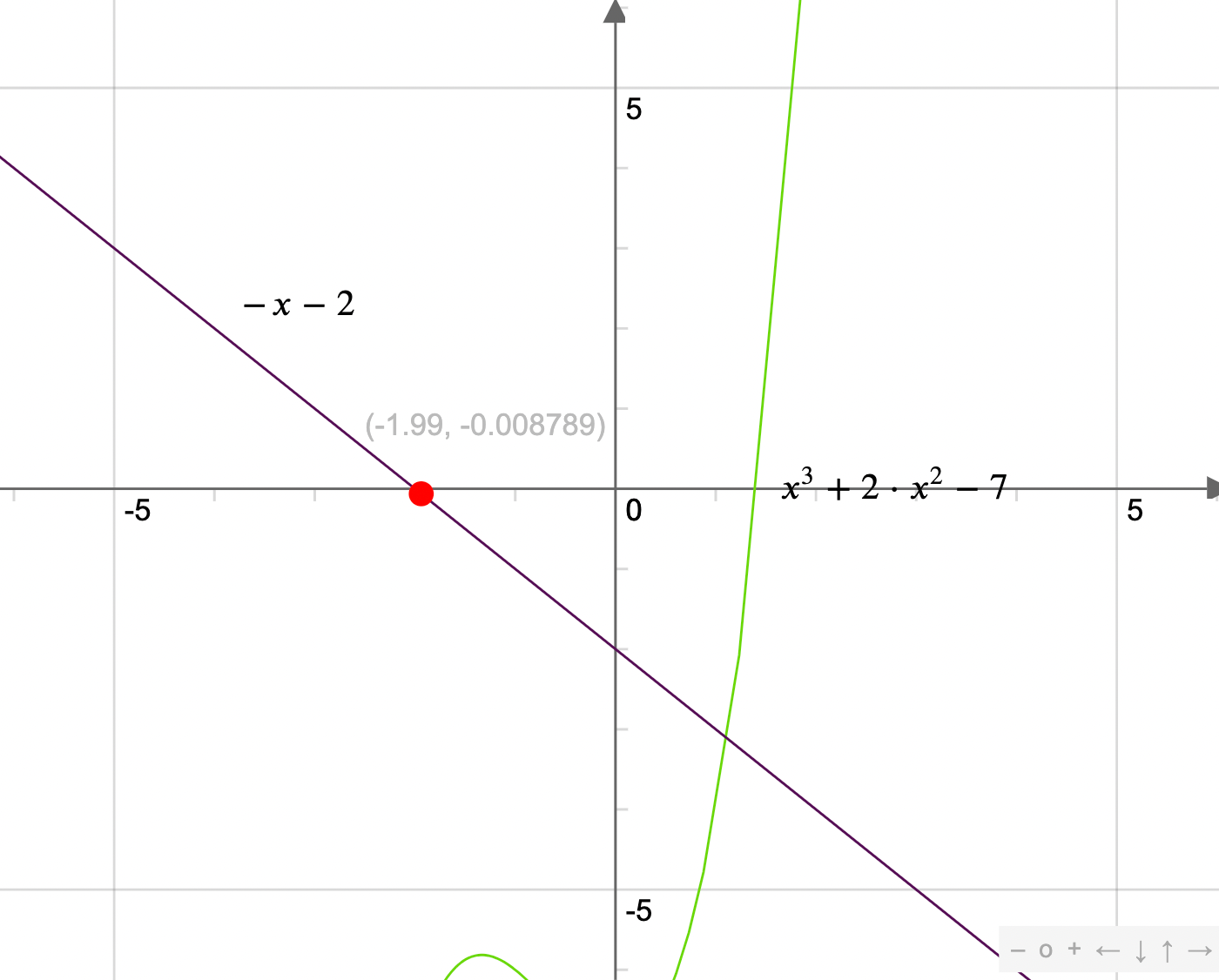
- A l'aide du graphique, déterminer l'équation réduite de la droite d. J'ai trouvé grâce au graphique que l'équation de la droite était -x-2.
-
@Hex Bonsoir,
L'équation réduite est fausse. Compare ton graphique et celui de l'énoncé, ils ne correspondent pas.
Les unités du graphique fournie ne sont pas 1.
Tu sais que f(0)=−7f(0) = -7f(0)=−7, donc l'équation réduite de la droite est
y = -x-7. (à justifier).Tu étudies ensuite le signe de x3+2x2−7−(−x−7)=x3+2x2+xx^3+2x^2-7 -(-x-7) = x^3+2x^2+xx3+2x2−7−(−x−7)=x3+2x2+x