Exercice de Maths, spé Terminal
-
HHyu dernière édition par
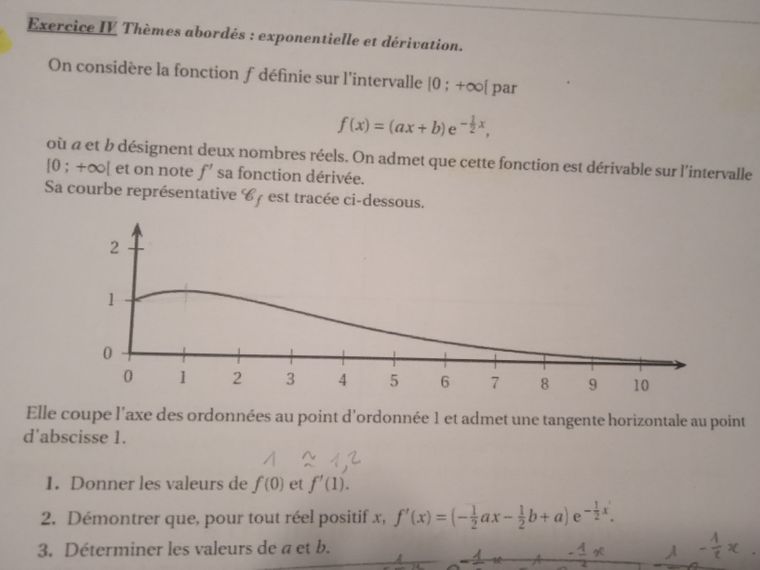
Bonjour, j'ai un DM à rendre sur les dérivation et les études de fonctions. Cependant, je n'arrive pas le dernier exercice :
f(x)= (aX+b)e^-1÷2×X
J'ai démontré avant que f'(X) = (-1÷2 ×aX-1÷2 ×b +a)e^-1÷2 ×X
(Je mets la photo en copie, c'est plus simple)Et il faut que je determine les valeurs de a et b.
Pouvez-vous m'aider ? Merci d'avance !!!
-
@Hyu Bonjour,
Utilises les résultats de la question 1 pour écrire un système de deux équations avec les inconnues aaa et bbb puis tu le résous.
f(0)=1f(0)= 1f(0)=1 donne b=..b= ..b=..
la valeur indiquée pour f′(1)f'(1)f′(1) est fausse : f′(1)=0f'(1) = 0f′(1)=0 vu que la tangente est horizontale.Je te laisse poursuivre les calculs. Indique les calculs et ou les résultats si tu souhaites une vérification.
-
HHyu dernière édition par
Bonjour @Noemi Je te remercie pour ta réponse.
Cependant, je ne comprends pas vraiment comment faire. Lorsque j'essaie de résoudre les équations à deux inconnus, je tombe sur des calculs insensés et que je ne sais pas résoudre.
Peux-tu m'aiguiller un peu plus (dans la limite du raisonnable bien sûr ^^) ?
-
f(0)=1f(0)= 1f(0)=1 donne be0=1be^0=1be0=1, soit b=1b= 1b=1
f′(1)=0f'(1) = 0f′(1)=0 donne (−12a−12b+a)e−12=0(-\dfrac{1}{2}a-\dfrac{1}{2}b+a)e^{-\frac{1}{2}}=0(−21a−21b+a)e−21=0
Un produit de facteur est nul si et seulement si l'un de ses facteurs est nul, comme l'exponentielle est non nulle, il reste.
(−12a−12b+a)=0(-\dfrac{1}{2}a-\dfrac{1}{2}b+a)=0(−21a−21b+a)=0
comme b=1b= 1b=1
cela donne
(12a−12)=0(\dfrac{1}{2}a-\dfrac{1}{2})=0(21a−21)=0 ; soit a=....a = ....a=....
-
mtschoon dernière édition par

Bonjour,
@Hyu , tu as de la chance que la modération n'ait pas supprimé ton scan d'énoncé, car en principe ils ne sont pas autorisés.
Une autre fois, scanne seulement le graphique (ce qui est autorisé)