Nombres premiers et diviseurs

Bonjour pouvez vous m'aider svp ?

Déterminer trois nombres premiers de la forme n^4 +m^4 où m et n désignent des entiers naturels.

Merci !

@momomo Bonjour,

C'est la seule question de l'exercice ?
As-tu testé des valeurs ?

Exemple : $1^4+2^4= ....$

Bonjour, oui c'est la seule question e l'exercice , j'ai trouvé 97,17 et 337 mais je ne sas pas comment justifier à part dire par tâtonnement je sais pas si je dois justifier avec de la congruence ...

@momomo

La justification est-elle demandée ?

oui,elle est demandée

@momomo

Tu dois justifier quoi ?
Que les nombres sont premiers ?

comment on a trouvé ces nombres

@momomo

Tu indiques les calculs que tu as fait et comment tu as vérifié que le nombre final était premier.

Bonjour,

@momomo , je te fais une suggestion :
disposition pratique : faire un tableau à double entrée.

En ligne, tu mets les valeurs naturelles de $m$ : 0,1,2,3,...
En colonne, tu mets les valeurs naturelles de $n$ : 0,1,2,3,...
Dans chaque case bleue tu mets la valeur de $n^4+m^4$

Tu construis le nombre de cases suffisant pour obtenir 3 nombres premiers (en rouge dans le schéma joint)
Tu peux t'arrêter à $m = 3$ et $n = 3$ , vu que tu as obtenu 3 nombres premiers $(2, 17, 97)$
S'il avait fallu 4 ou 5 nombres premiers, tu aurais dû faire un tableau plus grand.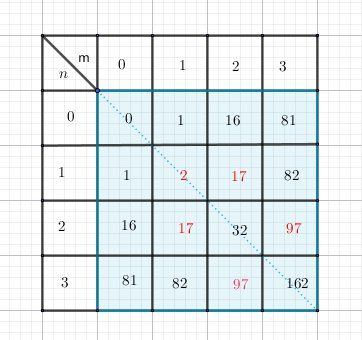

Ensuite pour chaque élément des cases bleues du tableau, tu fais les justifications demandées pour prouver "premier" ou "non premier" avec la méthode de ton choix.
$0$ et $1$ ne sont pas premiers (voir cours).
$2$ est premier
Pour les autres valeurs strictement supérieures à $2$ , tu peux remarquer que lorsque $n$ et $m$ ont la même parité, $n^4+m^4$ est pair donc multiple de $2$ donc non premier.
Il ne reste que les cas où $n$ et $m$ sont de parité différente à analyser