Déterminer l’abscisse du point P qui est l'intersection de la tangente et de l’axe des abscisses
-
lifiozor dernière édition par lifiozor
Bonjour !
Voici l'énoncé :
On considère la fonction f définie sur R par f(x) = −12x^3 + 164x^2 − 683x + 820.
On note C la courbe représentative de f dans un repère.- Déterminer une équation de la tangente T0 à C au point A0 d’abscisse x0 = 2,5
- Déterminer l’abscisse du point P intersection de T0 et de l’axe des abscisses.
Pour la question n°1, j'ai cherché la dérivée de f ce qui me donne f'(x)=-36x^2+328x-683
puis j'ai utilisé la formule y=f'(a)(x-a)+f(a) et cela me donne y=-88x+170
Mais je n'ai aucune idée de comment répondre à la question n°2
merci d'avance pour votre aide
-
@lifiozor Bonjour,
Pour la question 2, tu résous l'équation y=0y= 0y=0.
-
mtschoon dernière édition par mtschoon

Bonjour,
@lifiozor , l'équation de la tangente en A0A_0A0 que tu donnes est bien exacte.
Pour le point P, tu as dû trouver, avec l'indication de Noemi,
P(8544,0)P(\dfrac{85}{44},0)P(4485,0)8544≈1.93\dfrac{85}{44}\approx 1.934485≈1.93
Illustration graphique :
Courbe en bleu
Tangente en A0A_0A0 en rouge
A0(2.5,−50)A_0(2.5,-50)A0(2.5,−50)
P(8544,0)P(\dfrac{85}{44},0)P(4485,0)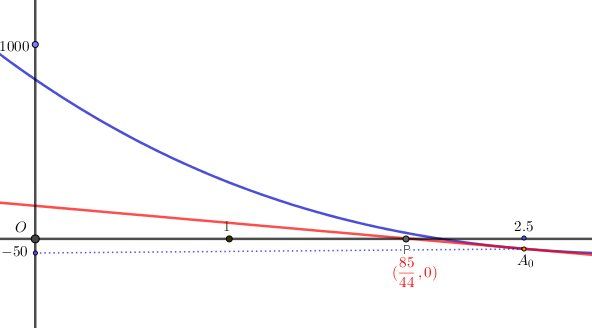
Evidemment , vu les données, il faut choisir des unités adaptées pour voir quelque chose..!