Suite numérique et proportion

Bonjour,

Je sèche sur la fin de ce problème.
En effet, j'ai trouvé la conjecture qui est a priori 1/2 mais sachant que la somme des carrés blancs est différente selon que n soit pair ou impair, je n1arrive pas á la démontrer...
Je vous remercie d'un petit coup de main éventuel....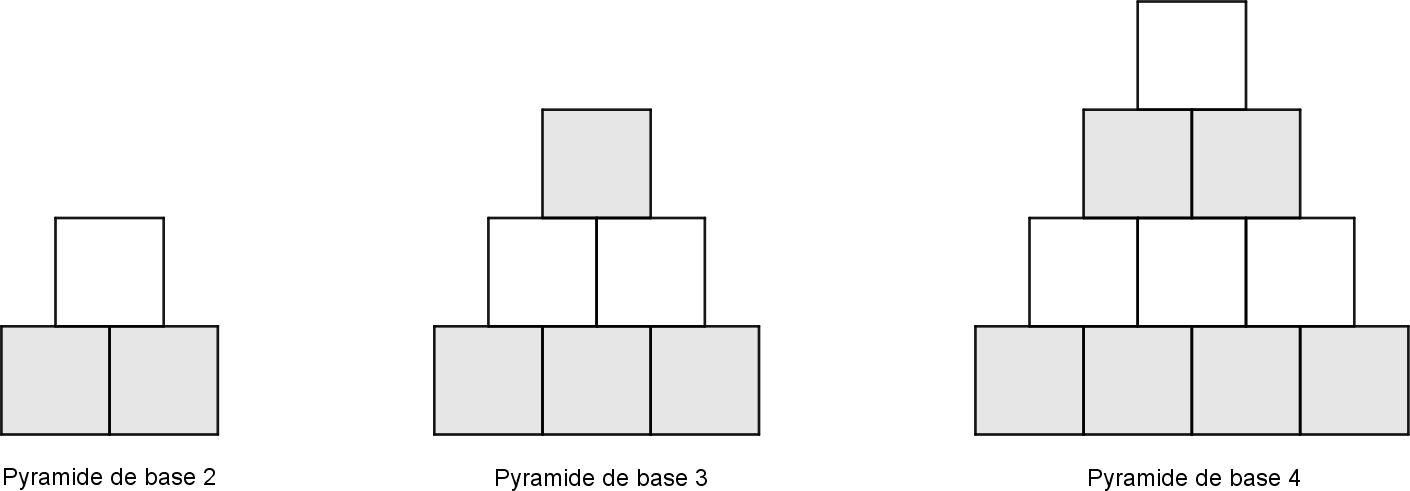

image TIRR.jpg

Construire et colorier les pyramides de bases 5, 6 et 7 comme celles de l’énoncé.
Pour chacune des pyramides de base 2, 3, 4, 5, 6 et 7, calculer la proportion de carrés blancs, c’est-à-dire la fraction de carrés de la pyramide qui ne sont pas coloriés. Que constate-t-on ?
Que peut-on conjecturer concernant les proportions de carrés blancs de la pyramide de base 25 ?
Étude d’un cas particulier
a. De combien de carrés est formée la pyramide de base 60 ?
b. Combien de carrés blancs comporte-t-elle ?
c. Quelle est la proportion de carrés blancs de cette pyramide ?
Recopier et compléter la conjecture suivante : « Plus on augmente le nombre de carrés de la base, plus la proportion de carrés blancs s’approche de … ».
Soit n un entier naturel supérieur à 1. Exprimer, en fonction de n,

a. le nombre de carrés qui forment la pyramide de base n,
b. le nombre de carré blancs de cette pyramide,
c. la proportion de carrés blancs de la pyramide de base n.

Démontrer alors la conjecture du 5.

@franckbudapest Bonjour,

Etudie les cas n pair puis n impair.

@Noemi
Bonjour,

Oui, c'est ce que j'ai tenté de faire, mais je ne parviens pas á démontrer la conjecture...

Bonjour,

@franckbudapest , je regarde un peu ce que tu indiques et ta difficulté,
Ta conjecture est bonne.
Soit $W_n)$ la suite correspondant aux proportions de carrés blancs

Si l'on observe de près :
$W2=W3=13W_2=W_3=\dfrac{1}{3}$

$W4=W5=25W_4=W_5=\dfrac{2}{5}$

$W6=W7=37W_6=W_7=\dfrac{3}{7}$
...
pour $p≥1p\ge 1$
$W2p=W2p+1=p2p+1W_{2p}=W_{2p+1}=\dfrac{p}{2p+1}$
La limite ( lorsque le nombre de carrés de la base de la pyramide tend vers $+∞+\infty$ ) est bien $12\dfrac{1}{2}$

@franckbudapest , quelques pistes pour les démonstrations (demandées à la question 6)

6 )a)
Soit $U_n)$ la suite correspondant aux nombres de carrés qui forment la pyramide de base $n$

$U_n=n+(n-1)+(n-2)+...+2+1$

$U_n$ est donc la somme des n permiers natyrels non nuls.
Tu as peut-être la formule directe dans ton cours :
$Un=n(n+1)2U_n=\dfrac{n(n+1)}{2}$

Sinon, tu utilises la somme des n premiers termes de la suite arithmétique de premier terme $1$ et de raison $1$

6)b)
Soit $V_n)$ la suite correspondant aux nombres de carrés blancs qui forment la pyramide de base $n$ .

Effectivement, comme tu l'as indiqué , il faut distinguer le cas de $n$ pair et de $n$ impair.

Je te fais le cas de $n$ pair
Soit $n = 2 p$ avec $p∈N∗p\in N^*$

$V_{2p}=(2p-1)+(2p-3)+...+5+3+1$

Il y a $p$ termes dans cette somme.

$V_{2p}$ est la somme des $p$ premiers termes de la suite arithmétique de raison 2, de premier terme 1 et de dernier terme $(2 p - 1)$

Donc :
$V2p=p×1+(2p−1)2V_{2p}=p\times\dfrac{1+(2p-1)}{2}$

Après simplification :
$V2p=p×2p2=p×p=p2V_{2p}=p\times \dfrac{2p}{2}=p\times p=\boxed{p^2}$

Je te laisse faire cas cas de $n$ impair, c'est-à-dire $n = 2 p + 1$ avec $p∈N∗p\in N^*$
Tu devrais trouver, sauf erreur : $V2p+1=p(p+1)V_{2p+1}=\boxed{p(p+1)}$

Pour la question 7)

$Wn=VnUnW_n=\dfrac{V_n}{U_n}$

Tu dois trouver la réponse qui a été conjecturée.

@mtschoon

Merci beaucoup, cela m'aide vraiment, je me relance dans ce travail demain et reposte si besoin.
Grand merci encore une fois.

De rien @franckbudapest et bon DM.

Reposte si tu butes quelque part.

Bonjour! Comment faut il trouver la conjecture?

@vlila , bonjour,

Une conjecture se trouve par observation des premiers résultats obtenus.

Consulte ma première intervention sur ce topic.

@mtschoon Merci!

De rien @vlila
Ta demande était modeste.