diamètre est le plus grand segment du cercle

[timo alex]

cercle c'est l'ensemble des points du disk aussi du périmètre,
D=max({d(m;n),∀m€(c),∀n€(c),∀r€]0;+infini [}).
quand m et n circule en tout mouvement dans le cercle,la liason le segment mn est toujours existant .leur dénombrement et leur ordination du plus petit au plus grand ,le sommet parmi eux ou leur borne supérieure c'est le diamètre lui même.je proposé la rédaction de prouvé cette proposition

[mtschoon]

@timo-alex bonjour/bonsoir

Ici , la politesse n'est pas une option, elle est obligatoire.
Il faudra y penser une autre fois.

Une piste rapide, si j'ai bien compris ta question.

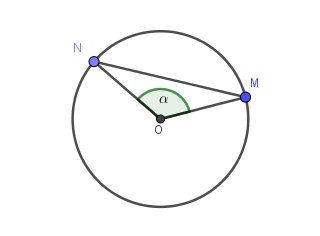
Cercle de centre $O$ et de rayon $R$
$MN$ corde du cercle

Tu démontres que $MN=2Rsin\frac{\alpha }{2}$

Le maximum de $MN$ est pour $sin\frac{\alpha }{2}=1$, c'est à dire $\frac{\alpha }{2}=\frac{\pi }{2}$ c'est à dire $\alpha =\pi$

Le maximum de $MN$ est donc $2R$, lorsque $O,M,N$ sont alignés : c'est le diamètre