calcule spirale d'or

bonjour
je dois calculer la longueur de la spirale constituée de 6 quarts de cercle obtenu à partir d'un rectangle initial de 15 centimètres de largeur.
Pouvez vous m'aider? Je suis bloqué
J'ai trouvé pour le premier arc de cercle
(2X15XPI)/4= (15PI)/2
Après je n'arrive pas à calculer les 5 autres
Merci pour votre aide

@meltim37 Bonjour,

As-tu fait une figure avec une échelle ?
Le nouveau rayon est la somme des deux précédents, sauf pour le deuxième qui est égal au double du premier.

indique tes calculs ou solutions si tu souhaites une vérification.

bonjour
je n'ai pas fait de figure car il me manque la longueur du carré.

Bonjour,

Je n'ai pas compris la réponse de Noemi.

Quant à la longueur du rectangle initial, elle est connue car ...
Il s'agit d'une spirale d'or ... donc construit à partir d'un rectangle dont le rapport longueur/largeur = $φ\varphi$ (le nombre d'or)

Avec $φ=1+52\varphi = \frac{1+\sqrt{5}}{2}$

Donc la longueur du rectangle initial est $\frac{1+\sqrt{5}}{2}$
Et le rayon du 2ème quart de cercle est : $\frac{1+\sqrt{5}}{2} - 15 = 15 * \frac{\sqrt{5}-1}{2}$

Avec un raisonnement analogue, on trouve :
Le rayon du 3ème quart de cercle est $(\frac{\sqrt{5}-1}{2})^2$

Le rayon du 4ème quart de cercle est $(\frac{\sqrt{5}-1}{2})^3$
...
Le rayon du n ième quart de cercle est $(\frac{\sqrt{5}-1}{2})^{n-1}$

On peut donc facilement trouver les longueurs des quarts de cercles correspondants.

Sauf si on a modifié la définition de la spirale d'or, ou que ma vieille mémoire me fait défaut.

Bonjour,

@meltim37 a dit dans calcule spirale d'or :

je n'ai pas fait de figure car il me manque la longueur du carré.

@meltim37 , la longueur du rectangle n'a pas d'importance.
Il suffit de prendre cette longueur strictement supérieure à la largeur (15 cm).
Tu prends la longueur égale à 20cm ou 25cm par exemple.

Pour faire la construction si tu as besoin, tu peux regarder ici :
il y a une construction qui se fait à la règle et au compas
https://www.youtube.com/watch?v=OxyMBlw1haA

@mtschoon a dit dans calcule spirale d'or :

la longueur du rectangle n'a pas d'importance.

Bonjour,

Pour moi, la longueur est imposée (voir mon message précédent)

@Black-Jack , bonjour,

Je viens de voir ta réponse.
@meltim37 le dira , mais je ne pense pas qu'il(elle) connaisse le nombre d'or...

Voir la construction proposée dans le lien
https://www.youtube.com/watch?v=OxyMBlw1haA

Il devrait correspondre à ce que cherche @meltim37

Le mieux est que @meltim37 indique son énoncé entier.

L

@mtschoon a dit dans calcule spirale d'or :

@Black-Jack , bonjour,

Je viens de voir ta réponse.
@meltim37 le dira , mais je ne pense pas qu'il(elle) connaisse le nombre d'or...

Rebonjour,

OK, mais le titre "Spirale d'or" est pourtant explicite ... ou devrait l'être.

Voir ici par exemple :

https://germea.pagesperso-orange.fr/nombre4.pdf

De plus, si la longueur n'est pas imposée, on ne peut pas calculer la longueur de la spirale constituée de ... comme demandé, sauf laisser la longueur du rectangle initial en littéral dans les calculs et aboutir à une "formule" indigeste et non numérique.

@Black-Jack , je ne te dis pas le contraire, mais il s'agit ici (je pense) d'une construction géométrique de cette spirale d'or, avant de faire les calculs.

Attendons la réponse de @meltim37 .

@mtschoon a dit dans calcule spirale d'or :

@Black-Jack , bonjour,

Je viens de voir ta réponse.
@meltim37 le dira , mais je ne pense pas qu'il(elle) connaisse le nombre d'or...

Voir la construction proposée dans le lien
https://www.youtube.com/watch?v=OxyMBlw1haA

Il devrait correspondre à ce que cherche @meltim37

Le mieux est que @meltim37 indique son énoncé entier.

L

Pour en terminer (pour moi)

Si on regarde le lien youtube et qu'on fait attention à la construction du rectangle initial à partir des manipulations du compas ...

La largeur mesure "2" et la longueur mesure $\sqrt{5}$ et donc ...

Bien sûr @Black-Jack !

Au départ, la largeur 15 cm est imposée et par construction, la longueur utile s'en déduit.

Mais, pour pouvoir démarrer, @meltim37 ne doit pas se "focaliser" sur la longueur.
Le "rectangle de départ" ne sert pas à la construction , vu que sa longueur semble être prise "au hasard".
Seule la largeur est connue.

*La construction proposée permet d'avoir la longueur utile du rectangle utile (en bref, du rectangle d'or).

Toute l'interrogation est sur ce "rectangle initialement donné" (? ? ?)**

Peut-être que @meltim37 a tout simplement mal formulé sa question.
Ce ne serait pas la première fois que ça arrive !

Comme déjà dit, le mieux est d'attendre l'énoncé complet de @meltim37.

bonjour
merci pour vos réponses, on connait la valeur du rectangle d'or car il y avait un exercice à faire avant sur le rectangle d'or.
Voici l'énoncé exact:
déterminer une valeur approchée à 10-3 près de la longueur de la spirale constituée de 6 quarts de cercle obtenu à partir d'un rectangle initial de 15 cm de largeur

@meltim37 a dit dans calcule spirale d'or :

bonjour
merci pour vos réponses, on connait la valeur du rectangle d'or car il y avait un exercice à faire avant sur le rectangle d'or.
Voici l'énoncé exact:
déterminer une valeur approchée à 10-3 près de la longueur de la spirale constituée de 6 quarts de cercle obtenu à partir d'un rectangle initial de 15 cm de largeur

on ne veut pas la tracer mais juste calculer sa longueur

@meltim37 ,

Merci d'avoir donner des explications.

ça charge tout si tu connais le rectangle d'or ! ! !

(il aurait été bien de dire dans ta question de départ que tu avais fait ,AVANT, un exercice sur le rectangle d'or."...ça aurait évité une discussion inutile...)

Tu peux donc faire la construction exacte de la spirale en partant du rectangle d'or.
http://www.clg-vivonne-rambouillet.ac-versailles.fr/IMG/pdf/nombre_d_or.pdf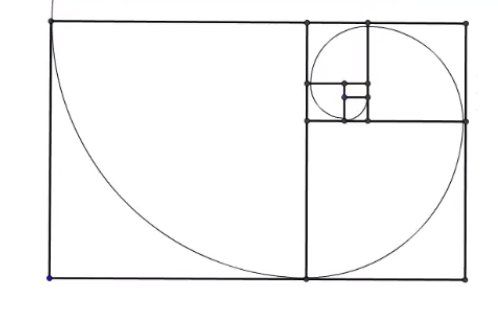

Tu calcules les rayons des 6 premiers quarts de cercles.
Tu en déduis les périmètres des 6 premiers quarts de cercles et tu fais la somme.

merci pour vos explications
je ne comprends pas beaucoup la longueur
c'est 15x (1+RACINE 5) : 2
ET pas 15+ (1+RACINE 5) : 2
et je ne comprends pas également le calcul du 2ieme quart de cercle

j'ai compris pourquoi la longueur est 15x (1+RACINE 5) : 2
ensuite pour calculer le rayon j'ai bien trouver 15X (1+RACINE 5) : 2 -15
mais je ne comprends comment c'est égale à 15X (racine5 - 1) : 2
pouvez vous m'aider

@meltim37 Bonjour,

Mets 15 en facteur et tu simplifies.

Bonjour,

@Noemi a dit dans calcule spirale d'or :

Mets 15 en facteur et tu simplifies.

En Latex:

$15×(1+52)−15=15×(1+52−1)15\times\biggr(\dfrac{1+\sqrt 5}{2}\biggr)-15=15\times\biggr(\dfrac{1+\sqrt 5}{2}-1\biggr)$

$15×(1+52)−15=15×(1+5−22)15\times\biggr(\dfrac{1+\sqrt 5}{2}\biggr)-15=15\times\biggr(\dfrac{1+\sqrt 5-2}{2}\biggr)$

donc
$15×(1+52)−15=15×(5−12)15\times\biggr(\dfrac{1+\sqrt 5}{2}\biggr)-15=15\times\biggr(\dfrac{\sqrt 5-1}{2}\biggr)$

@mtschoon merci j'avais fini par trouver
pour le périmètre 2 j'ai trouvé :
(15x( racine 5 -1) x pi) : 2= 14,562
pour le périmètre 3 :
$(15 x (3 - R A C I N E 5) x p i) : 4$ =9
pour périmètre 4:
$(15 x (r a c i n e 5 - 2) x p i) : 2$ =5, 562
pour périmètre 5 :
$(15 x (7 - 3 r a c i n e 5) x p i) : 4$ = 3,438
pour périmètre 6 :
$(15 x (- 11 + 5 r a c i n e 5) x p i) : 4$ = 2,125
pouvez vous me dire si c'est juste
merci à tous pour votre aide

@meltim37 , bonjour,

Oui, c'est bon, mais je me permets quelques remarques :

Bien sûr, n'oublie pas le périmètre 1 (que tu as déjà calculé) dans la somme.

Quand tu indiques des valeurs approchées, ne mets pas le symbole "=" ( qui n'est valable que pour des valeurs exactes).
Mets plutôt un symbole du genre $≈\approx$ qui veut dire "voisin de"

Pour calculer la somme demandée ( à $10^{-3}$ près), utilise les valeurs approchées avec le plus possibles de décimales que ta calculette donne pour chaque périmètre, et arrondis à $10^{-3}$ près seulement à la fin.
(Sinon, les décimales de la somme ne sont pas les bonnes...)
L'idéal serait de calculer la somme avec les valeurs irrationnelles exactes des périmètres et d'arrondir seulement après).

Fais au mieux !

@mtschoon merci beaucoup pour ton aide
Grâce à vous tous,j'ai pu finir mon exercice

Oui @meltim37 , plusieurs aidants ont participé.
C'est très bien ainsi.

Bon DM !