Equation logarithmique
-
safia adili dernière édition par
Bonsoir,
Je vous envoie ce message parce que je galère complètement sur une énoncé:Ln( X^2 - 2x + 1) - Ln( 3 - 2 x) = Ln (3)
A)-8
B)-2+2 racine de 3
C)8
D) Aucunes des propositionsPeut importe ce que je fais je tombe constamment sur la réponse B Mais la correction nous montre qu'il s'agit de la réponse A.
Est-ce que vous pouvez m'éclairer s'il vous plaît?
-
mtschoon dernière édition par mtschoon

@safia-adili, bonjour,
Que dire...
Je viens de faire la résolution, et je tombe aussi sur la réponse B (qui est une des deux solutions).
-
mtschoon dernière édition par mtschoon

@safia-adili , bonjour,
Je trouve, pour l'équation que tu indiques, deux solutions :
−2+23-2+2\sqrt 3−2+23 (c'est à dire la proposition B) et −2−23-2-2\sqrt 3−2−23Je t'indique des pistes,
L'équation peut s'écrire :
ln(x−1)2−ln(3−2x)=ln(3)ln(x-1)^2-ln(3-2x)=ln(3)ln(x−1)2−ln(3−2x)=ln(3)Conditions d'existence : x≠1x\ne 1x=1 et 3−2x>03-2x\gt 03−2x>0
D=]−∞,1[∪]1,32[D=\biggr]-\infty, 1\biggr[\cup\biggr]1,\dfrac{3}{2}\biggr[D=]−∞,1[∪]1,23[
Après transformations, sur DDD, l'équation équivaut à
x2+4x−8=0x^2+4x-8=0x2+4x−8=0
Les deux solutions sont −2+23-2+2\sqrt 3−2+23 et −2−23-2-2\sqrt 3−2−23 qui sont dans DDDIllustration graphique :
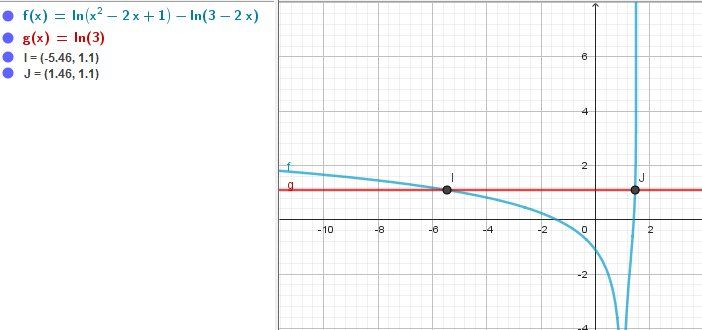
-
mtschoon dernière édition par

Remarque :
−8-8−8 (réponse A) ne peut pas être solution de l'équation proposée car si tu remplaces xxx par −8-8−8 , tu obtiens après calcul :
ln(8119)=ln(3)ln (\dfrac{81}{19})=ln(3)ln(1981)=ln(3) ce qui est FAUX
-
BBlack-Jack dernière édition par
Bonjour,
Peut être aussi une erreur de recopie dans l'énoncé.
Si l'équation avait été : ln(x²-2x+1)-ln(3-3x) = ln(3)
... alors il y a une unique solution qui est x = -8
-
safia adili dernière édition par
@mtschoon Bonjour,
Merci beaucoup !
-
mtschoon dernière édition par mtschoon

De rien @safia-adili .
Assure toi que l'énoncé que tu donnes est bien le bon.
Si l'énoncé est bon, le résultat B est une des deux solutions.
Si l'énoncé n'est pas bon, en le modifiant, comme Black-Jack le propose, le résultat A est la solution unique.