les vecteurs directeur

Bonjour,
désolé de vous déranger, je bloque sur un exo, est-ce que vous pouvez m'aider?
Voici l'énoncé:

"Dans le plan muni d'un repère orthonormé, soit d la droite d'équation 3x + 4y = 2 et soit e la droite d'équation 2x - y = 3. Soit f la droit parallèle à d qui passe par l'origine . Quelle est l'abscisse du point d'intersection des droites e et f ?

A)11/12
B)12/11
C)12/5
D)3"

Je ne sais absolument pas ce qu'il faut faire. Je suis perdu mais complètement. Est-ce que vous pouvez éclairer ma lanterne, s'il vous plaît?

@safia-adili , bonjour,
Un schéma pour t'éclairer

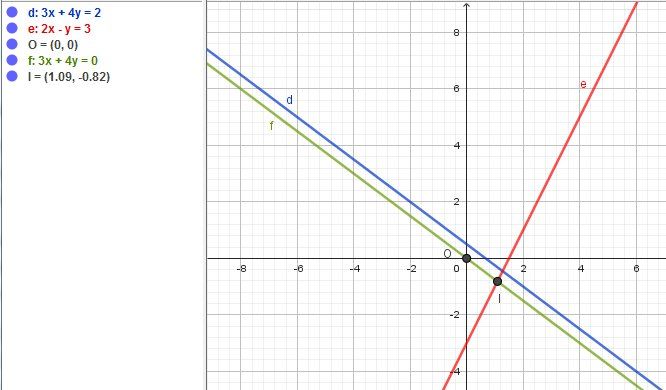
Soit I le point d'intersection de $(e)$ avec $(f)$

L'abscisse de $I$ est $1211\dfrac{12}{11}$ réponse $B$

Je t'indique une démarche :

Tu cherches l'équation de $(f)$ .
Vu que $(f)$ est parallèle à $(d)$ , tu peux utiliser le fait que ces deux droites ont même vecteur directeur de coordonnées $(- 4, 3)$
L'équation de $(f)$ peut s'écrire $3 x + 4 y = c^{'}$
Vuu que $(f)$ passe par $O (0, 0)$ , tu trouves $c^{'} = 0$
L'équation de $(f)$ peut s'écrire $3 x + 4 y = 0$

Pour trouver l'abscisse de $I$ , tu résous le système :
${2x−y=33x+4y=0\begin{cases}2x-y=3\cr3x+4y=0\end{cases}$

Tu dois trouver $x=1211x=\dfrac{12}{11}$ et $y=−911y=-\dfrac{9}{11}$

@mtschoon merci beaucoup je comprends mieux

@safia-adili , bonjour,

Tu indiques que tu comprends "mieux"...
J'en déduis que tu ne comprends pas "totalement".

Je détaille un peu plus.

Une équation cartésienne d'une droite $(D)$ peut s'écrire sous la forme $a x + b y = c$ , avec $a$ et $b$ non tous nuls.
Un vecteur directeur de $(D)$ est $U→(−b,a)\overrightarrow{U}(-b,a)$

Ici, $(d)$ a pour équation $3 x + 4 y = 2$ donc $a = 3$ et $b = 4$
$U→(−4,3)\overrightarrow{U}(-4,3)$ est un vecteur directeur de $(d)$

Soit $a^{'} x + b^{'} y = c^{'}$ équation de $(f)$
Vecteur directeur de $(f)$ : $U′→(−b′,a′)\overrightarrow{U'}(-b',a')$

Vu que $(e)$ est parallèle à $(d)$ , $(d)$ et $(f)$ ont mêmes vecteurs directeurs.
Ainsi , tu peux prendre $U′→=U→\overrightarrow{U'}=\overrightarrow{U}$
$(- b^{'}, a^{'}) = (- b, a)$ d'où $b^{'} = b$ et $a^{'} = a$

Une équation de $(f)$ peut s'écrire $3 x + 4 y = c^{'}$

Vu que $O$ appartient à $(f)$ , pour $x = 0$ et $y = 0$ ,on obtient $(3×0)+(4×0)=c′(3\times 0)+(4\times 0)=c'$ donc $c^{'} = 0$ donc (f) a pour équation $3x+4y=0\boxed{3x+4y=0}$

Si besoin, tu peux consulter ici :
https://www.logamaths.fr/equation-cartesienne-dune-droite-dans-le-plan/