étude et représentation graphique d'une fonction

[Maxime 174]

bonsoir j'ai un exercice que je n'arrive pas à comprendre et j'aimerais avoir des indications afin de commencer à traiter l'exercice.
soit la fonction f défini sur R par f(x)=((3x^2)+(ax)+b)/(x^2+1)

1. sachant que la courbe représentative de f passe par les points A (0;3) et B(1;5) démontrer que pour tout x : f( x)=((3x^2)+(4x)+3)/(x^2+1)

[Noemi]

@Maxime-174 Bonjour,

Utilise les coordonnées des points A et B, pour écrire un système.
Pour le point A :
$\frac{3\times 0^2+a\times 0+b}{0^2+1}=3$ ce qui donne $b=...$
Pour le point B :
....

Je te laisse poursuivre, indique tes calculs et/ou résultats si tu souhaites une vérification.

[mtschoon]

Bonjour,

@Maxime-174 , pour cette question 1) que tu donnes, la réponse à trouver est indiquée dans ton énoncé.
Tu dois trouver
$f(x)=\frac{3x^2+4x+3}{x^2+2}$ c'est à dire : $a=3$ et $b=4$

Pour le prouver, suis la piste de Noemi

Soit $(C_f)$ la représentation graphique de $f$

$A\in (C_f)$ <=>$f(0)=3$ <=> $b=3$
$B\in (C_f)$ <=> $f(1)=5$ <=> $\frac{3+a+b}{2}=5$
Tu as donc simplement à résoudre:
$\{\begin{array}{l}b=3\\ \frac{3+a+b}{2}=5\end{array}$

[mtschoon]

@Maxime-174 ,

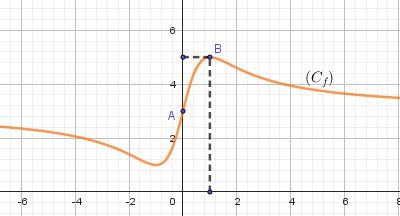
Illustration graphique :

[Maxime 174]

@mtschoon bonjour
Merci beaucoup pour vos explications je comprends mieux maintenant

[mtschoon]

De rien @Maxime-174 et bonne suite pour ton exercice.