aire segment de disque

J ai un ami qui doit calculer l aire d un segment de disque pour son travail. Et nous n avons que 2 dimensions la corde a= 126 et la hauteur
m = 90 après mes recherches on doit pouvoir trouver le rayon par la formule suivante
R= (m/2)+(a2/8m)
Est ce que quelqu'un peut me calculer cet aire et me donner le raisonnement merci Didier

@didier01500 Bonjour, (Marque de politesse à ne pas oublier !!)

Précise l'unité des valeurs indiquées.

Une piste :
Calcule :
Le rayon ;
L'angle du secteur angulaire ;
L'aire du secteur angulaire ;
L'aire du segment de disque.

Un lien : https://calculis.net/aire/segment-disque#resultat

Bonjour,

@didier01500 , je mets un schéma pour clarifier ton énoncé.

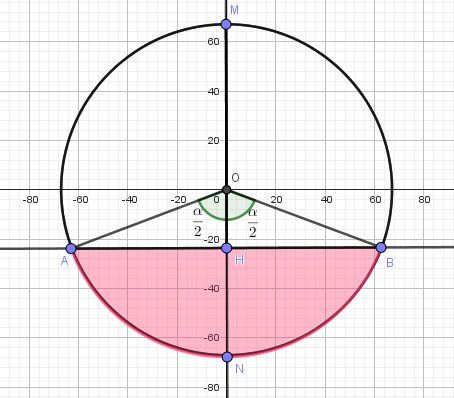
Si j'ai bien lu,

En unités de longueur,
$H M = m = 90$
$A B = a = 126$

Après calcul, avec la formule (exacte) que tu donnes,
$R=m2+a28mR=\dfrac{m}{2}+\dfrac{a^2}{8m}$ , tu dois trouver, sauf erreur, $R = 67.05$

Dans le triangle rectangle $A O H$ :
$sinα2=AHOA=6367.05sin\dfrac{\alpha}{2}=\dfrac{AH}{OA}=\dfrac{63}{67.05}$

En degrés, avec la fonction $sin^{-1}$ de ta calculette :
$α2=sin−1(6367.05)\dfrac{\alpha}{2}=sin^{-1}\biggr(\dfrac{63}{67.05}\biggr)$

Valeurs approchées en degrés ( tout dépend de la précision recherchée...)
$α2≈70\dfrac{\alpha}{2}\approx 70$ °
$AOB^=α\widehat{AOB}=\alpha$
$AOB^≈140\widehat{AOB}\approx 140$ °

Si c'est l'aire du segment circulaire (ANB) que tu cherches ( en rouge), tu calcules (avec la différence de deux aires) :
$aire(ANB)=παR2360−R22sinαaire(ANB)=\dfrac{\pi \alpha R^2}{360}-\dfrac{R^2}{2}sin\alpha$
Tu auras bien sûr cette aire en unités d'aire (associée à l'unité de longueur)

Sauf erreur, $(ANB)\approx 4048$ (unités d'aire).

Si c'est l'aire du segment circulaire (AMB) que tu cherches, tu fais
$aire(AMB)=πR2−aire(ANB)aire(AMB)=\pi R^2 -aire( ANB)$

Pour vérifier les réponses, je te conseille d'utiliser le calculateur que te propose Noemi.