Système avec des racines

Bonsoir a vous,

Je pose le contexte,

Dans le cadre de mes études supérieures je passe en CPGE - PTSI en septembre, afin de mieux apprehender cette année le futur professeur de mathématiques nous as donné des exercices a effectuer durant les vacances, or je bute sur une question, pourriez vous me donner des pistes afin de resoudre cette question s’il vous plaît ?

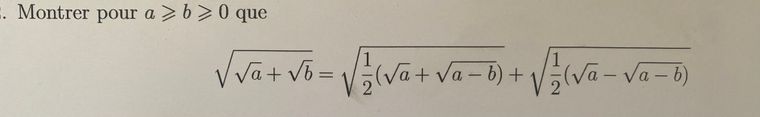
@Simon-Brassart Bonsoir,

On vérifie que chaque terme et positif, puis on élève chaque membre au carré.
Indique tes calculs si tu souhaites une vérification.

Bonsoir,
Merci beaucoup pour le conseil je teste ca et je n’hesiterai pas en envoyer mes recherches et mes calculs afin de pouvoir resoudre ce problème

Encore merci et bonne soirée a vous

@Noemi

Re bonjour,

Je reviens vers vous car je voit le bout dz la question mais je reste bloqué

Voila ce que je trouve apres avoir élevé au carré les deux termes et developpé l’identité remarquable.

Bonjour,

Comme te l'a demandé Noemi, tu as pu t'assurer qu'avec les conditions données dans l'énoncé, l'égalité proposée a bien un sens.

Tu as une égalité de la forme $A = B$ avec A et B positifs.
$A = B$ <=> $A^2=B^2$

Tu dois donc démontrer que :
$a+b=(12(a+a−b)+12(a−a−b)2\sqrt a+\sqrt b=\biggr(\sqrt{\dfrac{1}{2}(\sqrt{a}+\sqrt{a-b}})+\sqrt{\dfrac{1}{2}(\sqrt{a}-\sqrt{a-b}}\biggr)^2$

Je n'ai guère regardé ton brouillon, vu les ratures....!

Je te conseille de partir du membre de droite $(12(a+a−b)+12(a−a−b)2\biggr(\sqrt{\dfrac{1}{2}(\sqrt{a}+\sqrt{a-b}})+\sqrt{\dfrac{1}{2}(\sqrt{a}-\sqrt{a-b}}\biggr)^2$ , de le transformer avec les identités remarquables usuelles et tu dois trouver, au final, le membre de gauche $a+b\sqrt a+\sqrt b$

Soit $B2=(12(a+a−b)+12(a−a−b)2B^2=\biggr(\sqrt{\dfrac{1}{2}(\sqrt{a}+\sqrt{a-b}})+\sqrt{\dfrac{1}{2}(\sqrt{a}-\sqrt{a-b}}\biggr)^2$

Je te mets des pistes mais tu dois détailler beaucoup plus,

$B2=12(a+a−b)+12(a−a−b)+2(12(a+a−b))(12(a−a−b))B^2=\dfrac{1}{2}(\sqrt{a}+\sqrt{a-b})+\dfrac{1}{2}(\sqrt{a}-\sqrt{a-b})+2\biggr(\sqrt{\dfrac{1}{2}(\sqrt{a}+\sqrt{a-b}})\biggr)\biggr(\sqrt{\dfrac{1}{2}(\sqrt{a}-\sqrt{a-b}})\biggr)$

Tu simplifies :
$B2=a+(a+a−b)(a−a−b)B^2=\sqrt a+(\sqrt{\sqrt{a}+\sqrt{a-b}})(\sqrt{\sqrt{a}-\sqrt{a-b}})$

$B2=a+(a+a−b)(a−(a−b)B^2=\sqrt a+\sqrt{(\sqrt a+\sqrt{a-b})(\sqrt a -\sqrt{(a-b})}$

Tu dois voir une nouvelle identité remarquable sous le grand radical ,

Je te laisse l'utiliser et tu dois obtenir : $B2=a+bB^2=\sqrt a+\sqrt b$

Donc $B^2=A^2$ donc $A = B$

Bons calculs.
Reposte si besoin.

@mtschoon

Merci beaucoup

De rien @Simon-Brassart ,
J'espère que tu es arrivé à terminer le calcul sans difficulté.