Démontre que ((a+b)/2)^3 <=(a^3+b^3)/2
-
RRoy04 dernière édition par
Bonjour a tous. J'ai besoin d'aide sur cet exo (la question 2)
Exo- Développe (a+b)^3.
- On suppose que a et b sont positifs.
Démontre que ((a+b)/2)^3 <=(a^3+b^3)/2
-
@Roy04 Bonjour,
Pour la première question :
soit tu développes :(a+b)(a+b)2(a+b)(a+b)^2(a+b)(a+b)2
Soit tu connais la relation (x+y)3=x3+3x2y+.....(x+y)^3=x^3+3x^2y+.....(x+y)3=x3+3x2y+.....Pour la deuxième question
Exprime (a3+b32)(\dfrac{a^3+b^3}{2})(2a3+b3) à partir de la relation trouvée question 1.
(a3+b32)=(a+b)32−.....(\dfrac{a^3+b^3}{2})=\dfrac{(a+b)^3}{2}- .....(2a3+b3)=2(a+b)3−.....
-
RRoy04 dernière édition par
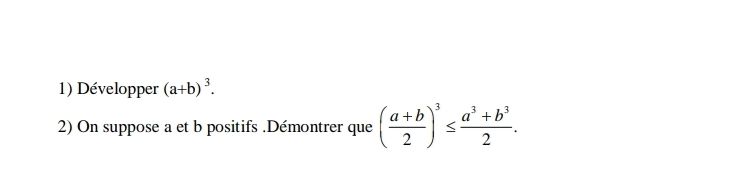
-
RRoy04 dernière édition par
Perci d'avoir répondu à mes questions.
Je comprends toujours pas comment parvenir à la démonstration de l'inégalité.
Et mes excuses car j'ai des difficultés pour insérer les écritures mathématiques.
Je viens de poster l'exo en image
-
RRoy04 dernière édition par
Ce message a été supprimé !
-
BBlack-Jack dernière édition par
Bonjour,
(a+b)³ = a³ + 3a²b + 3ab² + b³
((a+b)/2)³ = (a+b)³/8 = (a³ + 3a²b + 3ab² + b³)/8
((a+b)/2)³ - (a³+b³)/2 = (a³ + 3a²b + 3ab² + b³)/8 - (a³+b³)/2
((a+b)/2)³ - (a³+b³)/2 = (a³ + 3a²b + 3ab² + b³)/8 - (4a³+4b³)/8
((a+b)/2)³ - (a³+b³)/2 = (a³ + 3a²b + 3ab² + b³- 4a³ - 4b³)/8
((a+b)/2)³ - (a³+b³)/2 = (-3a³ + 3a²b + 3ab² -3b³)/8
((a+b)/2)³ - (a³+b³)/2 = (3a²(b-a) + 3b²(a -b))/8
((a+b)/2)³ - (a³+b³)/2 = (3a²(b-a) + 3b²(a -b))/8
((a+b)/2)³ - (a³+b³)/2 = 3.(b-a).(a² - b²)/8
((a+b)/2)³ - (a³+b³)/2 = 3.(b-a).(a - b)(a + b)/8
((a+b)/2)³ - (a³+b³)/2 = - 3.(a-b).(a - b)(a + b)/8
((a+b)/2)³ - (a³+b³)/2 = - 3.(a-b)².(a + b)/8 qui est <=0 avec a et b >= 0
Donc ((a+b)/2)³ - (a³+b³)/2 <= 0
((a+b)/2)³ <= (a³+b³)/2
-
RRoy04 dernière édition par
@Black-Jack c'est génial. Merci pour tout