exercice de somme et produit
-
tra va dernière édition par
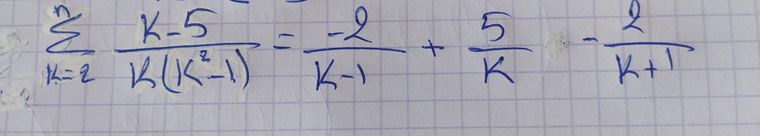
je sais pas comment la calculer
-
BBlack-Jack dernière édition par
Bonjour,
K−5K.(K2−1)=AK−1+BK+CK+1\frac{K-5}{K.(K^2-1)}= \frac{A}{K-1} + \frac{B}{K} + \frac{C}{K+1} K.(K2−1)K−5=K−1A+KB+K+1C
K-5 = A.K.(K+1) + B (K^2-1) + C.K.(K-1)
K-5 = K²(A+B+C) + K(A-C)-B
On identifie les termes de même puissance en K des 2 membres et on a le système :
A+B+C = 0
A-C = 1
B = 5Qui résolu donne : A = -2, B = 5 et C = -3
On a donc :
ΣK=2nK−5K(K2−1)=ΣK=2n[−2K−1+5K−3K+1]\displaystyle \Sigma_{K=2}^{n} \frac{K-5}{K(K^2-1)} = \Sigma_{K=2}^{n} [\frac{-2}{K-1} + \frac{5}{K} - \frac{3}{K+1}]ΣK=2nK(K2−1)K−5=ΣK=2n[K−1−2+K5−K+13]
Ce n'est pas tout à fait ce que tu as écrit.
Il reste évidemment à calculer la somme, soit en faisant les calculs adéquats, soit en se servant de ce qui a (peut-être) été fait avant dans l'exercice ... et pas noté ici.
Quel est l'énoncé COMPLET et EXACT ?
-
@tra-va Bonsoir, (Marque de politesse à ne pas oublier !!)
Utilise les sommes télescopiques.
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
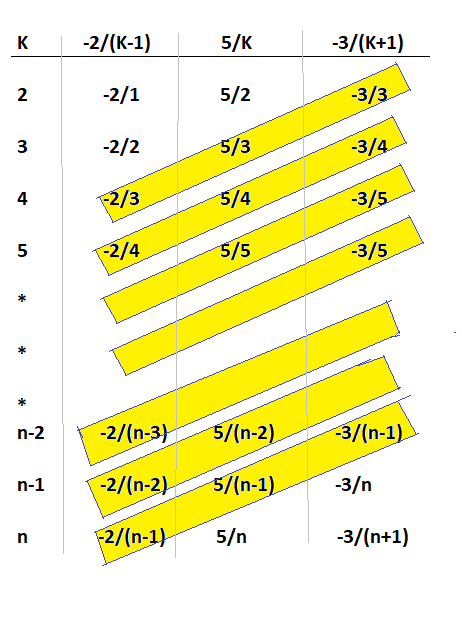
Essaie de comprendre ce dessin :
Les sommes dans les encadrés jaunes sont nulles ...
Il reste donc seulement les termes non encadrés, la somme totale vaut donc ...Attention à la valeur de n (si n = 2 ou 3 différent de si n >= 4)