Angles et droites parallèles

Salut et merci de m'avoir aidé
ABEF étant un trapèze isocèle inscrit dans un cercle de diamètre [EF] de centre O et tel que les angles OAE et EAB sont égaux.
Montrer que les droites (OA) et (BE) sont parallèles.

@galois Bonjour,

As tu fais une figure ?
Analyse les angles.

@Noemi oui j'ai une figure claire et j'ai essayé de trouver deux angles correspondants ou alternes-internes égaux mais j' ai pas pu

@galois

Quelle est la nature des triangles $O A F$ et $E A F$ ?

@Noemi aucune hypothèse n'est donnée pour ces triangles
J'ai remarqué que le premier est équilatéral mais j'ai pas pu prouver

@galois

Le triangle $E A F$ est inscrit dans un demi-cercle de diamètre $E F$ , donc il est rectangle.
Si tu calcules la mesure de l'angle $AEO^\widehat {AEO}$ , tu trouves 30°, donc l'angle $AFE^=60°\widehat {AFE}=60°$
Le triangle $A O F$ est équilatéral. Donc $A F = O A = R$ , le rayon du cercle.
Comme le trapèze est isocèle $A F = B E$ , tu peux indiquer que les triangles $E B O$ , $O B A$ et $O A F$ sont équilatéraux et conclure sur les droites.

@Noemi comment AEO = 30

@Noemi a dit dans Angles et droites parallèles :

@galois

Le triangle $E A F$ est inscrit dans un demi-cercle de diamètre $E F$ , donc il est rectangle.
Si tu calcules la mesure de l'angle $AEO^\widehat {AEO}$ , tu trouves 30°, donc l'angle $AFE^=60°\widehat {AFE}=60°$
Le triangle $A O F$ est équilatéral. Donc $A F = O A = R$ , le rayon du cercle.
Comme le trapèze est isocèle $A F = B E$ , tu peux indiquer que les triangles $E B O$ , $O B A$ et $O A F$ sont équilatéraux et conclure sur les droites.

Bonjour,

Oui, on trouve bien angle(AEO) = 30°, mais encore faut-il y arriver.

Personnellement cela m'a demandé une bonne dizaine de lignes de calculs (Pythagore, Al Kashi) et de manipulations de formules trigonométriques.

Il y a probablement plus direct ... mais cela m'a alors échappé.

@Black-Jack merci bien c'est très gentil

@galois

L'énoncé est-il complet ?

Bonjour,

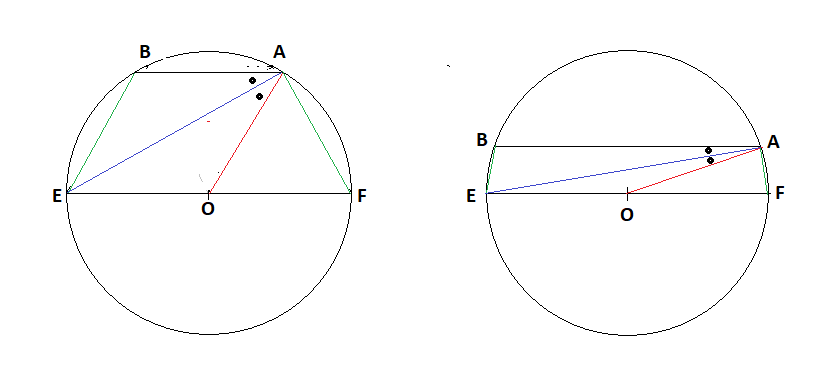
Il y a une bisbrouille dans l'énoncé.

On peut démontrer que si l'angle AEO mesure 30°, alors les droites (OA) et (BE) sont parallèles. (comme sur le dessin de gauche)

Mais, on a aussi les angles OAE et EAB égaux si l'angle AEO est différent de 30° ... mais alors on n'a plus les droites (OA) et (BE) parallèles. (comme sur le dessin de droite)

L'énoncé tel qu'il est écrit est donc faux (ou du moins incomplet)
Sans titre.png

@Black-Jack la figure à gauche est fournie dans les énoncés mais pas d'angle de 30 °

@galois

Donc tu en déduis que les droites $(O A)$ et $(B E)$ sont parallèles seulement si l'angle $AEO^\widehat {AEO}$ est égal à 30°.

@Noemi merci vivement

@galois a dit dans Angles et droites parallèles :

@Black-Jack la figure à gauche est fournie dans les énoncés mais pas d'angle de 30 °

Bonjour,

Voir, si sur le dessin de l'exercice, il n'y avait pas une indication supplémentaire à celle du texte.
Comme par exemple :
Un indication que AF = OF ou bien que AB = OF ou bien autre chose ...
qui permettrait alors de lever (par calcul) l'indétermination sur la valeur de l'angle AEO.

@Black-Jack non pas d'autre indication .c'est un exercice que j'ai trouvé dans un devoir